已知函数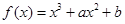
的图象上一点P(1，0)，且在P点处的切线与直线
平行．
(1)求函数
的解析式；
(2)求函数在区间[0，t](0<t<3)上的最大值和最小值；
(3)在(1)的结论下，关于x的方程
在区间[1,3]上恰有两个相异的实根，求实数c的取值范围
一个容量为M的样本数据，其频率分布表如下．
（Ⅰ）完成频率分布表 ；
（Ⅱ）画出频率分布直方图 ；
（Ⅲ）利用频率分布直方图，估计总体的众数、中位数及平均数．
【解】 频率分布表频率分布直方图
| 分组 |
频数 |
频率 |
| (10,20] |
2 |
0.10 |
| (20,30] |
3 |
|
| (30,40] |
4 |
0.20 |
| (40,50] |
||
| (50,60] |
4 |
0.20 |
| (60,70] |
2 |
0.10 |
| 合计 |
1.00 |
已知函数
（1）当
=
时，求曲线
在点（
,
）处的切线方程。
(2)若函数在（1，）上是减函数，求实数的取值范围；
（3）是否存在实数
若不存在，说明理由。若存在，求出的值，并加以证明。
已知椭圆的中心是坐标原点
，焦点在
轴上，离心率为
，又椭圆上任一点到两焦点的距离和为
．过右焦点
与轴不垂直的直线
交椭圆于
，
两点。
（1）求椭圆的方程；
（2）在线段
上是否存在点
,使得
？若存在，求出
的取值范围；若不存在，请说明理由.
如图示，边长为4的正方形
与正三角形
所在平面互相垂直，M、Q分别是PC，AD的中点。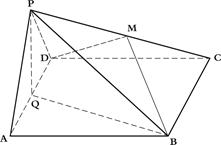
（1）求证： 
（2）求多面体
的体积
（3）试问：在线段AB上是否存在一点N，使面
若存在，指出N的位置，若不存在，请说明理由。
在等差数列{
}中，
=3，其前
项和为
，等比数列{
}的各项均为正数，
=1，公比为q,且b2+ S2=12，
．
（1）求与的通项公式；
（2）设数列{
}满足
，求{}的前n项和
．