如图，正方形ABCD的两条对角线把正方形分割成四个等腰直角三-优题课

如图，正方形ABCD的两条对角线把正方形分割成四个等腰直角三角形，将这四个三角形分别沿正方形ABCD的边向外翻折，可得到一个新正方形EFGH．请你在矩形ABCD中画出分割线，将矩形分割成四个三角形，然后分别将这四个三角形沿矩形的边向外翻折，使得图₁得到菱形，图₂得到矩形，图₃得到一般的平行四边形（只在矩形ABCD中画出分割线，说明分割线的作法，不画出翻折后的图形）．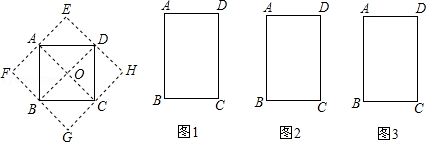

科目数学题型解答题难度中等

知识点：圆内接四边形的性质

九年三班的小雨同学想了解本校九年级学生对哪门课程感兴趣，随机抽取了部分九年级学生进行调查（每名学生必选且只能选择一门课程）．将获得的数据整理绘制如下两幅不完整的统计图．

根据统计图提供的信息，解答下列问题：

（1）在这次调查中一共抽取了　　名学生， $m$ 的值是　　．

（2）请根据以上信息直接在答题卡上补全条形统计图；

（3）扇形统计图中，“数学”所对应的圆心角度数是　　度；

（4）若该校九年级共有1000名学生，根据抽样调查的结果，请你估计该校九年级学生中有多少名学生对数学感兴趣．

经过校园某路口的行人，可能左转，也可能直行或右转．假设这三种可能性相同，现有小明和小亮两人经过该路口，请用列表法或画树状图法，求两人之中至少有一人直行的概率．

如图，在菱形 $ABCD$ 中，对角线 $AC$ 与 $BD$ 交于点 $O$ ．过点 $C$ 作 $BD$ 的平行线，过点 $D$ 作 $AC$ 的平行线，两直线相交于点 $E$ ．

（1）求证：四边形 $OCED$ 是矩形；

（2）若 $CE = 1$ ， $DE = 2$ ，则菱形 $ABCD$ 的面积是　　．

如图，已知 $A (- 2, 0)$ ， $B (4, 0)$ ，抛物线 $y = a x^{2} + bx - 1$ 过 $A$ 、 $B$ 两点，并与过 $A$ 点的直线 $y = - \frac{1}{2} x - 1$ 交于点 $C$ ．

（1）求抛物线解析式及对称轴；

（2）在抛物线的对称轴上是否存在一点 $P$ ，使四边形 $ACPO$ 的周长最小？若存在，求出点 $P$ 的坐标，若不存在，请说明理由；

（3）点 $M$ 为 $y$ 轴右侧抛物线上一点，过点 $M$ 作直线 $AC$ 的垂线，垂足为 $N$ ．问：是否存在这样的点 $N$ ，使以点 $M$ 、 $N$ 、 $C$ 为顶点的三角形与 $ΔAOC$ 相似，若存在，求出点 $N$ 的坐标，若不存在，请说明理由．

如图1，点 $E$ 是正方形 $ABCD$ 边 $CD$ 上任意一点，以 $DE$ 为边作正方形 $DEFG$ ，连接 $BF$ ，点 $M$ 是线段 $BF$ 中点，射线 $EM$ 与 $BC$ 交于点 $H$ ，连接 $CM$ ．

（1）请直接写出 $CM$ 和 $EM$ 的数量关系和位置关系；

（2）把图1中的正方形 $DEFG$ 绕点 $D$ 顺时针旋转 $45 °$ ，此时点 $F$ 恰好落在线段 $CD$ 上，如图2，其他条件不变，（1）中的结论是否成立，请说明理由；

（3）把图1中的正方形 $DEFG$ 绕点 $D$ 顺时针旋转 $90 °$ ，此时点 $E$ 、 $G$ 恰好分别落在线段 $AD$ 、 $CD$ 上，如图3，其他条件不变，（1）中的结论是否成立，请说明理由．