如图,四棱锥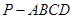 中,
中,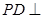 平面
平面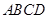 ,底面
,底面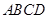 为矩形,
为矩形, 为
为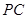 的中点.
的中点.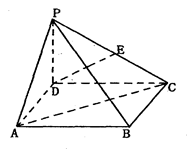
(1)求证: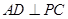 ;
;
(2)在线段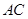 上是否存在一点
上是否存在一点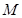 ,使得
,使得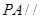 平面
平面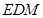 ?若存在,求出
?若存在,求出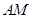 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(1)用反证法证明:在一个三角形中,至少有一个内角大于或等于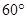 ;
;
(2)已知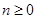 ,试用分析法证明:
,试用分析法证明: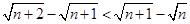 .
.
已知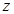 为复数,且
为复数,且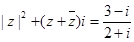 (
(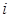 为虚数单位),求
为虚数单位),求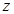 .
.
第17届亚运会将于2014年9月18日至10月4日在韩国仁川进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
(1)根据调查数据制作2×2列联表;
(2)根据列联表的独立性检验,能否认为性别与喜爱运动有关?
| 参考数据 |
当 时,无充分证据判定变量 时,无充分证据判定变量 有关联,可以认为两变量无关联; 有关联,可以认为两变量无关联; |
当 时,有 时,有 把握判定变量 把握判定变量 有关联; 有关联; |
|
当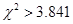 时,有 时,有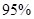 把握判定变量 把握判定变量 有关联; 有关联; |
|
当 时,有 时,有 把握判定变量 把握判定变量 有关联. 有关联. |
(参考公式: ,其中
,其中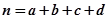 .)
.)
已知 .
.
(1)求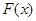 的单调区间;
的单调区间;
(2)求函数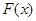 在
在 上的最值.
上的最值.