已知函数f(x)=x3+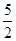 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+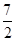 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).
(1)若g(x)在x=l处的切线方程为y=kx-5(k为常数),求b的值;
(2)设函数f(x)的导函数为 ,若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
,若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)令F(x)=f(x)-g(x),若函数F(x)存在极值,且所有极值之和大于5+1n2,求a的取值范围.
在锐角 中,
中, 、
、 、
、 分别为角
分别为角 所对的边,且
所对的边,且 .
.
(Ⅰ)确定角 的大小;
的大小;
(Ⅱ)若 =
= , 且
, 且 的面积为
的面积为 
 , 求
, 求 的值.
的值.
已知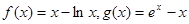 .
.
(Ⅰ)求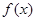 的最小值;
的最小值;
(Ⅱ)若存在 ,使不等式
,使不等式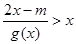 成立,求
成立,求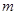 的取值范围;
的取值范围;
(Ⅲ)当 时,证明:
时,证明: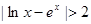 .
.
已知椭圆 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为 .
.
(Ⅰ)求椭圆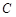 的标准方程;
的标准方程;
(Ⅱ)设不过原点 的直线
的直线 与椭圆
与椭圆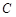 交于两点
交于两点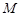 、
、 ,且直线
,且直线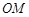 、
、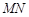 、
、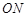 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△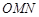 面积的取值范围.
面积的取值范围.
我市某校某数学老师这学期分别用 两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如下:
两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如下: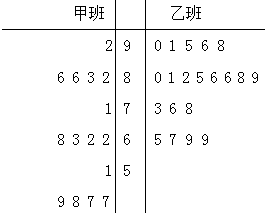
(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班所抽数学成绩不低于80分的同学中随机抽取两名同学,用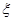 表示抽到成绩为86分的人数,求
表示抽到成绩为86分的人数,求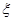 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)学校规定:成绩不低于85分的为优秀,作出分类变量成绩与教学方式的 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
下面临界值表仅供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
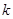 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: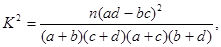 其中
其中 )
)
如图,正三棱柱 中,
中, 是
是 的中点,
的中点, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的平面角的余弦值.
的平面角的余弦值.