有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=4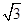 .将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= 度;
(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.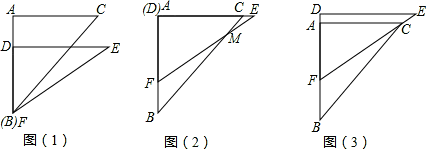

交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
情境观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是▲,∠CAC′=▲°.
问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.
在 中,
中,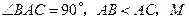 是
是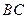 边的中点,
边的中点,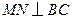 交
交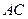 于点
于点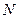 .动点
.动点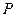 从点
从点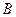 出发沿射线
出发沿射线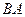 以每秒
以每秒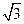 厘米的速度运动.同时,动点
厘米的速度运动.同时,动点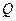 从点
从点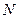 出发沿射线
出发沿射线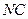 运动,且始终保持
运动,且始终保持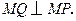 设运动时间为
设运动时间为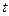 秒(
秒(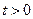 ).
).
(1)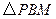 与
与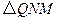 相似吗?以图1为例说明理由;
相似吗?以图1为例说明理由;
(2)若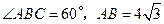 厘米.
厘米.
①求动点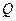 的运动速度;
的运动速度;
②设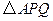 的面积为
的面积为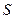 (平方厘米),求
(平方厘米),求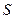 与
与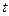 的函数关系式;
的函数关系式;
(3)探求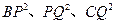 三者之间的数量关系,以图1为例说明理由.
三者之间的数量关系,以图1为例说明理由.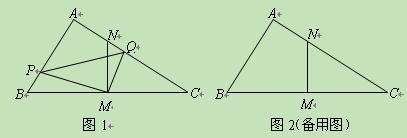
如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度 (厘米)与注水时间
(厘米)与注水时间 (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(1)图2中折线 表示________槽中水的深度与注水时间的关系,线段
表示________槽中水的深度与注水时间的关系,线段 表示_______槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点
表示_______槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点 的纵坐标表示的实际意义是________________________________;
的纵坐标表示的实际意义是________________________________;
(2)注水多长时间时,甲、乙两个水槽中水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112立方厘米,求甲槽底面积(壁厚不计).(直接写出结果)