已知四边形ABCD为平行四边形，BC⊥平面ABE，AE⊥BE，BE =" BC" = 1，AE = 
，M为线段AB的中点，N为线段DE的中点，P为线段AE的中点。
（1）求证：MN⊥EA；
（2）求四棱锥M – ADNP的体积。
(本小题8分)
设函数f(x)=x2-2x+2 ,x∈[t,t+1],t∈R,求函数f(x)的最小值g(t)的表达式.
(本小题8分)
设函数f(x)=x2-2x+2 ,x∈[t,t+1],t∈R,求函数f(x)的最小值g(t)的表达式.
(本小题8分)
已知集合A=｛x｜1-a<x<1+a｝,B=｛x｜-1<x<7｝,若A∩B=A,求a的取值范围.
(本小题12分)
已知
,
(1)判断
的奇偶性并用定义证明；
(2)当
时，总有
成立，求
的取值范围.
(本小题8分)
设函数
是定义域在
的函数，且
，对于任意的实数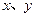
，都有
，当
>0时，
.
(1)求
的值；
(2)判断函数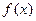
在的单调性并用定义证明；
(3)若
，解不等式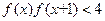
.