设椭圆C: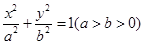 的两个焦点为F1、F2,点B1为其短轴的一个端点,满足
的两个焦点为F1、F2,点B1为其短轴的一个端点,满足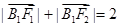 ,
,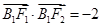 。
。
(1)求椭圆C的方程;
(2)过点M  做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。
做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。
已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切,直线
相切,直线 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求 的取值范围;
的取值范围;
定义在R上的奇函数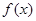 有最小正周期4,且
有最小正周期4,且 时,
时,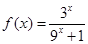 。
。
(1)求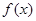 在
在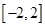 上的解析式;
上的解析式;
(2)判断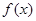 在
在 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当 为何值时,关于方程
为何值时,关于方程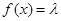 在
在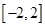 上有实数解?
上有实数解?
我省某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值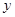 万元与投入
万元与投入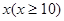 万元之间满足:
万元之间满足: 为常数。当
为常数。当 万元时,
万元时, 万元;
万元;
当 万元时,
万元时, 万元。(参考数据:
万元。(参考数据: )
)
(1)求 的解析式;
的解析式;
(2)求该景点改造升级后旅游利润 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。
已知函数 .
.
(1)若函数 的定义域和值域均为
的定义域和值域均为 ,求实数
,求实数 的值;
的值;
(2)若 在区间
在区间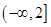 上是减函数,且对任意的
上是减函数,且对任意的 ,总有
,总有 ,求实数
,求实数 的取值范围;
的取值范围;
已知 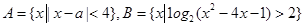
(1)若 =l,求
=l,求 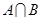 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.