某幼儿园在“六·一儿童节”开展了一次亲子活动，此次活动由宝宝和父母之一（后面以家长代称）共同完成，幼儿园提供了两种游戏方案：
方案一 宝宝和家长同时各抛掷一枚质地均匀的正方体骰子（六个面的点数分别是1，2，3，4，5，6），宝宝所得点数记为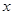
,家长所得点数记为
;
方案二 宝宝和家长同时按下自己手中一个计算器的按钮(此计算器只能产生区间［1，6］的随机实数)，宝宝的计算器产生的随机实数记为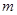
,家长的计算器产生的随机实数记为
.
(Ⅰ) 在方案一中，若
,则奖励宝宝一朵小红花，求抛掷一次后宝宝得到一朵小红花的概率；
（Ⅱ）在方案二中，若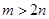
,则奖励宝宝一本兴趣读物，求按下一次按钮后宝宝得到一本兴趣读物的概率.
某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题：
(1)求分数在[50,60)的频率及全班人数；
(2)求分数在[80,90)之间的频数，并计算频率分布直方图中[80,90)间的矩形的高.
已知函数
.
（1）求
的单调递增区间；
（2）若
是第二象限角，
，求
的值.
如图所示，P是△ABC内一点，且满足
+
+
=
，设Q为CP延长线与AB的交点，求证：
=
.
已知向量
，函数
，且
的图像过点
和点
.
（1）求
的值；
（2）将的图像向左平移
个单位后得到函数
的图像，若图像上各最高点到点
的距离的最小值为1，求的解析式.
已知函数
，
.
（1）求
的最小正周期；
（2）求在闭区间
上的最大值和最小值.