设 分别为直角坐标系中与
分别为直角坐标系中与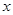 轴、
轴、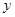 轴正半轴同方向的单位向量,若向量
轴正半轴同方向的单位向量,若向量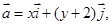
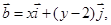 且
且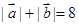 .
.
(Ⅰ)求点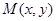 的轨迹
的轨迹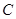 的方程;
的方程;
(Ⅱ)设抛物线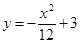 的顶点为
的顶点为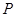 ,焦点为
,焦点为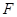 .直线
.直线 过点
过点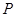 与曲线
与曲线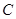 交于
交于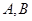 两点,是否存在这样的直线
两点,是否存在这样的直线 ,使得以
,使得以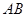 为直径的圆过点
为直径的圆过点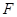 ,若存在,求出直线方程;若不存在,请说明理由?
,若存在,求出直线方程;若不存在,请说明理由?
某校为调研学生的身高与运动量之间的关系,从高二男生中随机抽取100名学生的身高数据,得到如下频率分布表:
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
[160,165) |
10 |
0.100 |
| 第2组 |
[165,170) |
① |
0.150 |
| 第3组 |
[170,175) |
30 |
② |
| 第4组 |
[175,180) |
25 |
0.250 |
| 第5组 |
[180,185) |
20 |
0.200 |
| 合计 |
100 |
1.00 |
(1)求频率分布表中①、②位置相应的数据;
(2)为了对比研究学生运动量与身高的关系,学校计划采用分层抽样的方法从第2、5组中随机抽取7名学生进行跟踪调研,求第2、5组每组抽取的学生数?
(3)在(2)的前提下,学校决定从这7名学生中随机抽取2名学生接受调研访谈,求至少有1名学生来自第5组的概率?
如图,已知多面体 中,平面
中,平面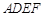 ⊥平面
⊥平面 ,若四边形
,若四边形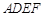 为矩形,
为矩形,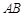 ∥
∥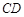 ,
,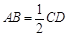 ,
,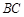 ⊥
⊥ ,
, 为
为 中点.
中点.
(1)求证: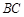 ⊥平面
⊥平面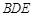 ;
;
(2)求证: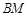 //平面
//平面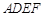 .
.
如图,在平面直角坐标系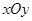 中,以
中,以 轴为始边作角
轴为始边作角 和
和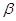 ,
,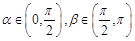 ,其终边分别交单位圆于
,其终边分别交单位圆于 两点.若
两点.若 两点的横坐标分别是
两点的横坐标分别是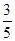 ,
,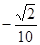 .试求
.试求
(1) ,
, 的值;
的值;
(2) 的值.
的值.
设函数f(x)=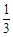 x3-
x3- x2+bx+c,曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
x2+bx+c,曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
(1)求b,c的值;
(2)已知 ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
| 分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
| 频数 |
3 |
4 |
8 |
15 |
| 分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 频数 |
15 |
x |
3 |
2 |
乙校:
| 分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
| 频数 |
1 |
2 |
8 |
9 |
| 分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
| 频数 |
10 |
10 |
y |
3 |
(1)计算x,y的值;
(2)若规定考试成绩在[120, 150]内为优秀,请分别估计两所学校数学成绩的优秀率;
(3)由以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.10的前提下
认为两所学校的数学成绩有差异.
| 甲校 |
乙校 |
总计 |
|
| 优秀 |
|||
| 非优秀 |
|||
| 总计 |
参考数据与公式: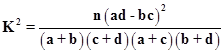
临界值表
| P(K2≥k0) |
0.10 |
0.05 |
0.010 |
| k0 |
2.706 |
3.841 |
6.635 |