已知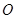 为坐标原点,点
为坐标原点,点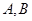 分别在
分别在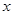 轴
轴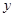 轴上运动,且
轴上运动,且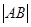 =8,动点
=8,动点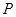 满足
满足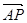 =
=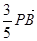 ,设点
,设点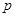 的轨迹为曲线
的轨迹为曲线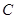 ,定点为
,定点为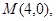 直线
直线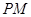 交曲线
交曲线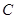 于另外一点
于另外一点 .
.
(1)求曲线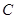 的方程;
的方程;
(2)求 面积的最大值.
面积的最大值.
设 ,其中
,其中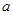 为正实数
为正实数
(1)当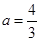 时,求
时,求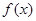 的极值点;
的极值点;
(2)若 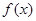 为R上的单调函数,求
为R上的单调函数,求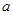 的取值范围.
的取值范围.
已知抛物线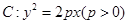 的焦点F和椭圆
的焦点F和椭圆 的右焦点重合。
的右焦点重合。
(1 )求抛物线C的方程,并求其准线方程;
)求抛物线C的方程,并求其准线方程;
(2)设P(1,2),是否存在平行于OP(O为坐标原点)的直线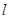 ,使得直线
,使得直线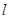 与抛物线
与抛物线
C有公共点,且直线OP与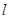 的距离等于
的距离等于 ?若存在,求出直线
?若存在,求出直线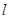 的方程;若不存在,
的方程;若不存在,
说明理由。
某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
5 |
0.050 |
| 第2组 |
 |
① |
0.350 |
| 第3组 |
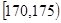 |
30 |
② |
| 第4组 |
 |
20 |
0.200 |
| 第5组 |
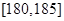 |
10 |
0.100 |
| 合计 |
100 |
1.00 |

如图,在三棱柱 中,底面
中,底面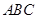 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱 面
面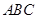 ,点
,点 是
是 的中点.
的中点.
(1)求证: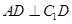 ;(2)求证:
;(2)求证: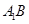 ∥平面
∥平面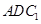

(1)求函数 的导数
的导数
(2)已知 ,求
,求 及
及