(Ⅰ)已知复数z=1﹣i(i是虚数单位),若z2+a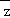 +b=3﹣3i,求实数a,b的值.
+b=3﹣3i,求实数a,b的值.
(Ⅱ)求二项式(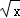 +
+ )10展开式中的常数项.
)10展开式中的常数项.
(本小题满分14分)如图,已知三棱锥A—BPC中,AP⊥PC, AC⊥BC,M为AB中点,D为PB中点, 且△PMB为正三角形.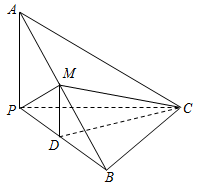
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D—BCM的体积.
(本小题满分14分)已知向量 ,
, 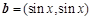 ,
, 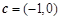 .
.
(1)若 ,求向量
,求向量 ,
, 的夹角
的夹角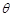 ;
;
(2)若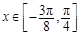 ,函数
,函数 的最大值为
的最大值为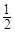 ,求实数
,求实数 的值.
的值.
(本小题满分为16分)数列 ,
,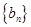 ,
, 满足:
满足: ,
, ,
,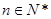 .
.
(1)若数列 是等差数列,求证:数列
是等差数列,求证:数列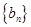 是等差数列;
是等差数列;
(2)若数列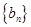 ,
, 都是等差数列,求证:数列
都是等差数列,求证:数列 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列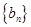 是等差数列,试判断当
是等差数列,试判断当 时,数列
时,数列 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
(本小题满分为16分)已知函数 .
.
(1)若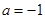 ,求函数
,求函数 的极值,并指出极大值还是极小值;
的极值,并指出极大值还是极小值;
(2)若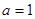 ,求函数
,求函数 在
在 上的最值;
上的最值;
(3)若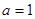 ,求证:在区间
,求证:在区间 上,函数
上,函数 的图象在
的图象在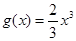 的图象下方.
的图象下方.
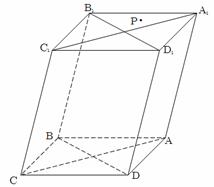
(本小题满分为14分) 如图,过四棱柱 形木块上底面内的一点
形木块上底面内的一点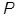 和下底面的对角线
和下底面的对角线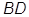 将木块锯开,得到截面
将木块锯开,得到截面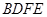 .
.
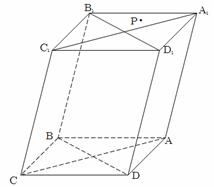
(1)请在木块的上表面作出过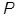 的锯线
的锯线 ,并说明理由;
,并说明理由;
(2)若该四棱柱的底面为菱形,四边形 是矩形时,试证明:平面
是矩形时,试证明:平面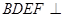 平面
平面 .
.