已知复数z=1﹣i(i是虚数单位)
(Ⅰ)计算z2;
(Ⅱ)若z2+a ,求实数a,b的值.
,求实数a,b的值.
(本小题10分)全集 ,若集合
,若集合 ,
, ,则
,则
(1)求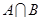 ,
,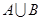 ;
;
(2)若集合C=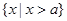 ,满足
,满足 时,求
时,求 的取值范围;(结果用区间或集合表示)[
的取值范围;(结果用区间或集合表示)[
(本小题满分14分)已知{an}是等差数列,其前n项的和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=21,S4+b4=30.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.
(本小题满分16分)已知函数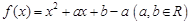 .
.
(1)若关于 的不等式
的不等式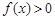 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(2)设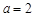 ,若不等式
,若不等式 对任意实数
对任意实数 都成立,求实数
都成立,求实数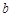 的取值范围;
的取值范围;
已知函数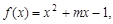
(1)若对于任意的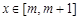 ,都有
,都有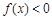 成立,求实数
成立,求实数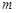 的取值范围;
的取值范围;
(2)如果关于x的不等式f(x)£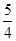 m有解,求实数m的取值范围.
m有解,求实数m的取值范围.
已知△ABC中,A,B,C所对的边分别为a,b,c,已知m=(sin C,sin Bcos A),n=(b,2c),且m·n=0.
(1)求A的大小;
(2)若a=2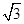 ,c=2,求△ABC的面积S的大小.
,c=2,求△ABC的面积S的大小.