设集合
.记
为同时满足下列条件的集合
的个数:
①
;②若
,则
;③若
,则
.
(1)求
;
(2)求
的解析式(用
表示).
借助“世博会”的东风,某小商品公司开发一种纪念品,每件产品的成本是15元,销售价是20元,月平均销售 件,通过改进工艺,产品的成本不变,质量得到提高,市场分析的结果表明:如果产品的销售价提高的百分率为
件,通过改进工艺,产品的成本不变,质量得到提高,市场分析的结果表明:如果产品的销售价提高的百分率为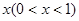 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为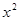 ,记改进工艺后,该公司销售纪念品的月平均利润是
,记改进工艺后,该公司销售纪念品的月平均利润是 元.
元.
(1)写出 与
与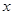 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该纪念品的销售价,使得公司销售该纪念品的月平均利润最大.
设椭圆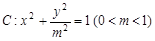 的左、右焦点分别为
的左、右焦点分别为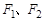 。过
。过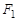 的直线
的直线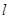 交
交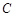 于
于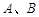 两点,且
两点,且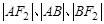 成等差数列.
成等差数列.
(1)求 ;(2)若直线
;(2)若直线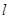 的斜率为1,求
的斜率为1,求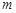 .
.
某校的研究性学习小组为了研究中学生的身高与性别情况,在该校随机抽出80名17至18周岁的学生,其中身高 的男生有30人,女生4人;身高<170的男生有10人。
的男生有30人,女生4人;身高<170的男生有10人。
(1)根据以上数据建立一个 列联表:
列联表:
(2)请问在犯错误的概率不超过0.001的前提下,该校17至18周岁的学生的身高与性别是否有关?
参考公式: 
参考数据:
已知函数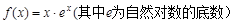
(1)求函数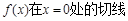 方程;
方程;
(2)求函数 的单调区间.
的单调区间.
已知复数
(1)若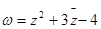 ,求
,求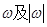 ;
;
(2)若 ,求实数
,求实数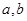 .
.