如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.

如图,矩形ABCD和梯形BEFC所在平面互相垂直,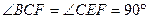 ,
,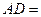
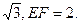
(1)求证: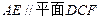 ;
;
(2)求证: ;
;
(3)当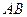 的长为何值时,二面角
的长为何值时,二面角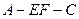 的大小为60°?
的大小为60°?
如图,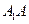 是圆柱的母线,
是圆柱的母线,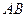 是圆柱底面圆的直径,
是圆柱底面圆的直径,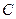 是底面圆周上异于
是底面圆周上异于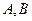 的任意一点,
的任意一点,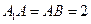 .(Ⅰ)求证:
.(Ⅰ)求证: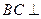 平面
平面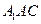 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥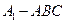 的体积的最大值.
的体积的最大值.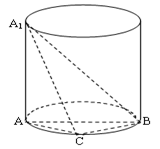
已知直线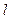 过点A(6,1)与圆
过点A(6,1)与圆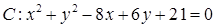 相切,
相切,
(1)求该圆的圆心坐标及半径长 (2)求直线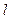 的方程
的方程
已知函数 定义域为
定义域为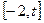 (
(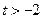 ),设
),设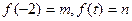 .
.
(1)试确定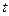 的取值范围,使得函数
的取值范围,使得函数 在
在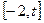 上为单调函数;
上为单调函数;
(2)求证: ;
;
(3)求证:对于任意的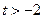 ,总存在
,总存在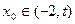 ,满足
,满足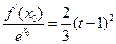 ,并确定这样的
,并确定这样的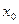 的个数.
的个数.
已知无穷数列 中,
中,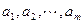 是首项为
是首项为 ,公差为
,公差为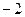 的等差数列;
的等差数列; 是首项为
是首项为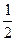 ,公比为
,公比为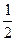 的等比数列
的等比数列 ,并对任意
,并对任意 ,均有
,均有 成立,(1)当
成立,(1)当 时,求
时,求 ;(2)若
;(2)若 ,试求
,试求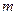 的值;(3)判断是否存在
的值;(3)判断是否存在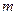 ,使
,使 成立,若存在,求出
成立,若存在,求出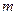 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.