某校为了探索一种新的教学模式，进行了一项课题实验，甲班为实验班，乙班为对比班，甲乙两班的人数均为50人，一年后对两班进行测试，测试成绩的分组区间为[80，90）、[90，100）、[100，110）、[110，120）、[120，130），由此得到两个班测试成绩的频率分布直方图：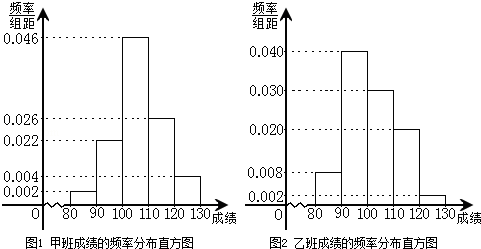
（Ⅰ）完成下面2×2列联表，你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗？并说明理由；
| |
成绩小于100分 |
成绩不小于100分 |
合计 |
| 甲班 |
a= _________ |
b= _________ |
50 |
| 乙班 |
c=24 |
d=26 |
50 |
| 合计 |
e= _________ |
f= _________ |
100 |
附：K2=
，其中n=a+b+c+d
| P（K2≥k0） |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
2.072 |
2.706 |
3.841 |
5.204 |
6.635 |
7.879 |
10.828 |
已知函数
，
（1）若曲线
与
在公共点
处有相同的切线，求实数
、
的值；
（2）当
时，若曲线与在公共点
处有相同的切线，求证：点唯一；
（3）若
，，且曲线与总存在公切线，求正实数的最小值
已知中心在原点，焦点在坐标轴上的双曲线
经过
、
两点
（1）求双曲线的方程；
（2）设直线
交双曲线于
、
两点，且线段
被圆
：
三等分，求实数
、
的值
已知公差不为0的等差数列
的前3项和
＝9，且
成等比数列
（1）求数列的通项公式和前n项和
；
（2）设
为数列
的前n项和，若
对一切
恒成立，求实数
的最小值
四边形
与
都是边长为
的正方形，点E是
的中点，
平面
（1）求证：
平面
；
（2）求证：平面
平面；
（3）求三棱锥A—BDE的体积
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆)，若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
（1）求下表中z的值；
（2）用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下：94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数
记这8辆轿车的得分的平均数为
，定义事件
{
，且函数
没有零点}，求事件
发生的概率