在某高校自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为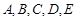
五个等级.某考场考生的两科考试成绩数据统计如下图所示，其中“数学与逻辑”科目的成绩为
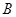的考生有
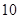人.
（Ⅰ）求该考场考生中“阅读与表达”科目中成绩为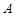
的人数；
（Ⅱ）若等级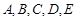分别对应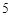
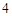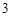分，
分，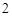
分，
分，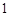
分，求该考场考生“数学与逻辑”科目的平均分；
（Ⅲ）已知参加本考场测试的考生中，恰有两人的两科成绩均为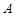.在至少一科成绩为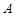的考生中,随机抽取两人进行访谈，求这两人的两科成绩均为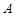的概率.
在
中，角A、B、C的对边分别为
.已知
.
（1）若
，求的面积；
（2）设向量
，
，且
，求
的值.
（本小题满分10分）选修4—5：不等式选讲
已知a＋b＝1，对
，b∈（0，＋∞），
＋
≥｜2x－1｜－｜x＋1｜恒成立，
（Ⅰ）求＋的最小值；
（Ⅱ）求x的取值范围。
（本小题满分10分）选修4—4：坐标系与参数方程
已知直线l经过点P（
，1），倾斜角α＝
，圆C的极坐标方程为
＝
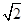cos（θ－
）．
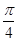（Ⅰ）写出直线l的参数方程，并把圆C的方程化为直角坐标方程；
（Ⅱ）设l与圆C相交于A，B两点，求点P到A，B两点的距离之积．
（本小题满分10分）选修4—1：几何证明选讲如图，四边形ACED是圆内接四边形，AD、CE的延长线交于点B，且AD＝DE，AB＝2AC．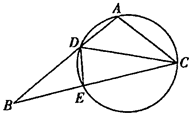
（Ⅰ）求证：BE＝2AD；
（Ⅱ）当AC＝2，BC＝4时，求AD的长．
（本小题满分12分）
已知函数f（x）＝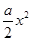
－bx＋lnx（a，b∈R）．
（Ⅰ）若a＝b＝1，求f（x）点（1，f（1））处的切线方程；
（Ⅱ）设a＜0，求f（x）的单调区间；
（Ⅲ）设a＜0，且对任意的x＞0，f（x）≤f（2），试比较ln（－a）与－2b的大小．