(本小题满分12分)
已知函数f(x)=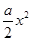 -bx+lnx(a,b∈R).
-bx+lnx(a,b∈R).
(Ⅰ)若a=b=1,求f(x)点(1,f(1))处的切线方程;
(Ⅱ)设a<0,求f(x)的单调区间;
(Ⅲ)设a<0,且对任意的x>0,f(x)≤f(2),试比较ln(-a)与-2b的大小.
(本小题满分12分)
已知,椭圆C以过点A(1,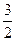 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。

(本小题满分13分)
已知A,B分别为曲线C: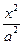 +
+ =1(y
=1(y 0,a>0)与x轴
0,a>0)与x轴
的左、右两个交点,直线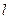 过点B,且与
过点B,且与 轴垂直,S为
轴垂直,S为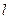 上
上
异于点B的一点,连结AS交曲线C于点T.
(1)若曲线C为半圆,点T为圆弧 的三等分点,试求出点S的坐标;
的三等分点,试求出点S的坐标;
(II)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在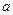 ,使得O,M,S三点共线?若存在,求出a的值,若不存在,请说明理由。
,使得O,M,S三点共线?若存在,求出a的值,若不存在,请说明理由。

(本小题满分12分)
已知椭圆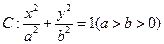 的离心率为
的离心率为 ,过右焦点F的直线
,过右焦点F的直线 与
与 相交于
相交于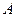 、
、 两点,当
两点,当 的斜率为1时,坐标原点
的斜率为1时,坐标原点 到
到 的距离为
的距离为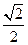
(I)求 ,
, 的值;
的值;
(II) 上是否存在点P,使得当
上是否存在点P,使得当 绕F转到某一位置时,有
绕F转到某一位置时,有 成立?
成立?
若存在,求出所有的P的坐标与 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
(本小题满分12分)

已知椭圆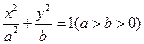 的左、右焦点分别为
的左、右焦点分别为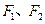 ,离心率
,离心率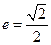 ,右准线方程为
,右准线方程为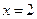 。
。
(I)求椭圆的标准方程;
(II)过点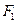 的直线
的直线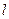 与该椭圆交于
与该椭圆交于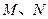 两点,且
两点,且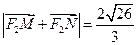 ,求直线
,求直线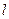 的方程。
的方程。
(本小题满分14分)
已知椭圆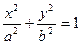 (
(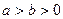 )的两个焦点分别为
)的两个焦点分别为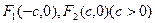 ,过点
,过点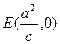 的直线与椭圆相交于点A,B两点,且
的直线与椭圆相交于点A,B两点,且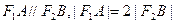
(Ⅰ求椭圆的离心率;
(Ⅱ)直线AB的斜率;
(Ⅲ)设点C与点A关于坐标原点对称,直线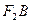 上有一点H(m,n)(
上有一点H(m,n)(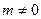 )在
)在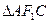 的外接圆上,求
的外接圆上,求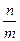 的值。
的值。