(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l经过点P( ,1),倾斜角α=
,1),倾斜角α= ,圆C的极坐标方程为
,圆C的极坐标方程为 =
=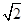 cos(θ-
cos(θ-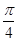 ).
).
(Ⅰ)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(Ⅱ)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积.
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ)求X的分布列; (Ⅱ)求X的数学期望E(X).
设p:实数x满足 ,其中
,其中 ,命题
,命题 实数x
实数x
满足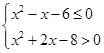
(Ⅰ)若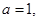 且
且 为真,求实数
为真,求实数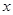 的取值范围;
的取值范围;
(Ⅱ)若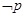 是
是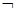
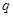 的充分不必要条件,求实数
的充分不必要条件,求实数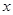 的取值范围.
的取值范围.
(本小题14分)已知函数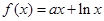
 .
.
(1)若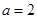 ,求曲线
,求曲线 在
在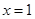 处切线的斜率;
处切线的斜率;
(2)求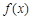 的单调区间;
的单调区间;
(3)设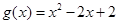 ,若对任意
,若对任意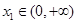 ,均存在
,均存在 ,使得
,使得 ,求
,求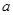 的取值范围。
的取值范围。
(本小题满分12分) 设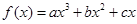 的极小值为
的极小值为 ,其导函数
,其导函数 的图像开口向下且经过点
的图像开口向下且经过点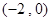 ,
, .
.
(Ⅰ)求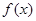 的解析式;(Ⅱ)方程
的解析式;(Ⅱ)方程 有唯一实数解,求
有唯一实数解,求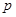 的取值范围.
的取值范围.
(Ⅲ)若对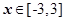 都有
都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 .
.
(1)若函数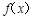 在(
在(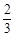 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
(2)是否存在正整数a,使得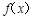 在(
在(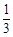 ,
, )上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
)上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.