设 奇函数,且对任意的实数
奇函数,且对任意的实数 当
当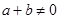 时,都有
时,都有
(1)若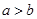 ,试比较
,试比较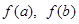 的大小;
的大小;
(2)若存在实数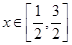 使得不等式
使得不等式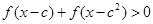 成立,试求实数
成立,试求实数 的取值范围.
的取值范围.
(本小题满分14分)设{an}是等差数列,{bn}是各项都为正数的等比数列,且
a1=b1=1,a3+b5=21,a5+b3=13.
(Ⅰ)求{an},{bn }的通项公式;
}的通项公式;
(Ⅱ)求数列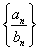 的前n项和
的前n项和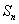 .
.
(本小题满分12分)如下图所示,某海轮以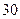 海里/小时的速度航行,在
海里/小时的速度航行,在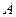 点测得海面上油井
点测得海面上油井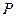 在南偏东
在南偏东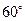 ,向北航行
,向北航行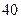
 分钟后到达
分钟后到达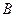 点,测得油井
点,测得油井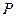 在南偏东
在南偏东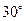 ,海轮改为北偏东
,海轮改为北偏东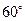 的航向再行驶
的航向再行驶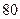 分钟到达
分钟到达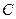 点,求
点,求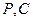 间的距离.
间的距离.
(本小题满分12分)
在△ABC中,BC=a,AC=b,a,b是方程x2—2 x+2=0的两个根,
x+2=0的两个根,
且2cos(A+B)=1.
求:(1)C的度数; (2)AB的长度; (3)△ABC的面积.
(本小题满分12分)(1) 为等差数列{an}的前n项和,
为等差数列{an}的前n项和,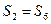 ,
, ,求
,求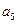 .
.
(2)在等比数列 中,
中,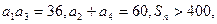 求
求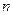 的范围
的范围
(本小题满分12分)解下列不等式:
(1)-x2+2x- >0;
>0;  (2)9x2-6x+1≥0.
(2)9x2-6x+1≥0.