如图，菱形ABCD中，对角线AC，BD相交于点O，且AC=6cm，BD=8cm，动点P，Q分别从点B，D同时出发，运动速度均为1cm/s，点P沿B→C→D运动，到点D停止，点Q沿D→O→B运动，到点O停止1s后继续运动，到B停止，连接AP，AQ，PQ．设△APQ的面积为y（cm2）（这里规定：线段是面积0的几何图形），点P的运动时间为x（s）．
（1）填空：AB= cm，AB与CD之间的距离为 cm；
（2）当4≤x≤10时，求y与x之间的函数解析式；
（3）直接写出在整个运动过程中，使PQ与菱形ABCD一边平行的所有x的值．
(1)如图，小明画了一个角∠MON＝80°，点A、B分别在射线OM、ON上移动，△AOB的角平分线AC和BD交与点P，小明通过测量，发现不论怎样变换点A、B的位置，∠APB的度数不发生改变，一直都是130°，请你解释其中的原因。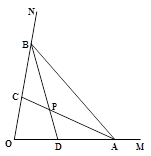
（2）小明想明白后，又开始考虑下图中的问题：△AOB的内角平分线AC和外角平分线BD所构成的∠C是不是也与∠AOB有特数的关系呢？如果∠AOB＝n°，那么∠C是多少度呢？请说明理由。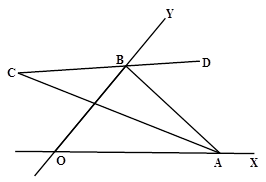
为了防控甲型H1N1流感，某校积极进行校园环境消毒，购买了甲、乙两种消毒液共100瓶，其中甲种6元/瓶，乙种9元/瓶．
（1）如果购买这两种消毒液共用780元，求甲、乙两种消毒液各购买多少瓶？
（2）该校准备再次购买这两种消毒液（不包括已购买的100瓶），使乙种瓶数是甲种瓶数的2倍，且所需费用不多于1200元（不包括780元），求甲种消毒液最多能再购买多少瓶？
已知，如图，在直角三角形ABC中，∠ACB=900，D是AB上一点，且∠ACD=∠B
（1）判断△ACD的形状？并说明理由。
（2）你在证明你的结论过程中应用了哪一对互逆的真命题？
在解方程组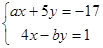
时，由于粗心，甲看错了方程组中的a，而得到解为
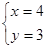；乙看错了方程组中的b而得到解为
。
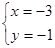（1）求正确的a、b值；
（2）求原方程组的解。
如图，∠1=250，∠B=650，AB⊥AC。
（1）AD与BC有怎样的位置关系？为什么？
（2）根据题中的条件，能判断AB与CD平行吗？如果能，请说明理由；如果不能，还应添加什么条件？