已知函数
(
为常数)的图像与
轴交于点
,曲线
在点
处的切线斜率为
.
(1)求
的值及函数
的极值;
(2)证明:当
时,
;
(3)证明:对任意给定的正数 ,总存在 ,使得当 时,恒有 .
已知曲线
上的点到点
的距离比它到直线
的距离小
.
(1)求曲线
的方程;
(2)曲线
在点
处的切线
与
轴交于点
.直线
分别与直线
及
轴交于点
,以
为直径作圆
,过点
作圆
的切线,切点为
,试探究:当点
在曲线
上运动(点
与原点不重合)时,线段
的长度是否发生变化?证明你的结论.
根据世行2013年新标准,人均GDP低于1035美元为低收入国家;人均GDP为1035-4085元为中等偏下收入国家;人均GDP为4085-12616美元为中等偏上收入国家;人均GDP不低于12616美元为高收入国家.某城市有5个行政区,各区人口占该城市人口比例及人均GDP如下表: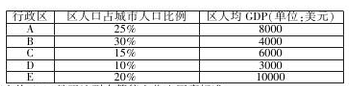
(1)判断该城市人均GDP是否达到中等偏上收入国家标准;
(2)现从该城市5个行政区中随机抽取2个,求抽到的2个行政区人均GDP都达到中等偏上收入国家标准的概率.
如图,三棱锥
中,
,
.
(1)求证:
;
(2)若
,
为
中点,求三棱锥
的体积.
已知函数
.
(1)求
的值;
(2)求函数
的最小正周期及单调递增区间.