定义在区间(0, )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有 .
.
(1)求证:方程f(x)=0有且只有一个实根;
(2)若a>b>c>1,且a、b、c成等差数列,求证: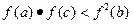 ;
;
(3)(本小题只理科做)若f(x) 单调递增,且m>n>0时,有 ,求证:
,求证: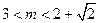
已知函数 在区间[0,1]上单调递增,在区间[1,2]上单调递减;
在区间[0,1]上单调递增,在区间[1,2]上单调递减;
(1)求a的值;
(2)求证:x=1是该函数的一条对称轴; (3)是否存在实数b,使函数
(3)是否存在实数b,使函数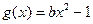 的图象与函数f(x)的图象恰好有两个交点?若存在,求出b的值;若不存在,请说明理由.
的图象与函数f(x)的图象恰好有两个交点?若存在,求出b的值;若不存在,请说明理由.
函数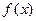 的定义域为R,并满足以下条件:①对任意
的定义域为R,并满足以下条件:①对任意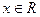 ,有
,有 ;
;
②对任意 、
、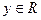 ,有
,有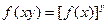 ;③
;③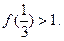 则
则
(1)求 的值;
的值;
(2)求证: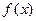 在R上是单调增函数;
在R上是单调增函数;
(3)若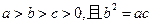 ,求证:
,求证:
已知函数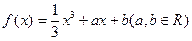 在
在 处取得的极小值是
处取得的极小值是 .
.
(1)求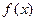 的单调递增区间;
的单调递增区间;
(2)若 时,有
时,有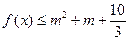 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设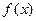 是定义在
是定义在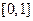 上的函数,若存在
上的函数,若存在
 ,使得
,使得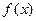 在
在 上单调递增,在
上单调递增,在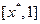 上单调递减,则称
上单调递减,则称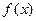 为
为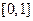 上的单峰函数,
上的单峰函数, 为峰点,包含峰点的区间为含峰区间. 对任意的
为峰点,包含峰点的区间为含峰区间. 对任意的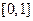 上的单峰函数
上的单峰函数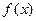 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(1)证明:对任意的
 ,
, ,若
,若 ,则
,则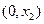 为含峰区间;若
为含峰区间;若 ,则
,则 为含峰区间;
为含峰区间;
(2)对给定的 ,证明:存在
,证明:存在
 ,满足
,满足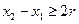 ,使得由(1)所确定的含峰区间的长度不大于
,使得由(1)所确定的含峰区间的长度不大于 ;
;