如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.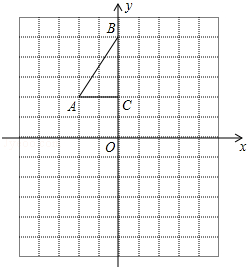
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.
(1)求证:BD=CD;
(2)若AE=6,BF=4,求⊙O的半径;
(3)在(2)条件下判断△ABC的形状,并说明理由.
如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD= .
.
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点P(x,y)在函数y=-x+5图象上的概率.
钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动.如图,一艘海监船位于钓鱼岛D的北偏东60°方向,与钓鱼岛的距离为16海里的A处,它沿正南方向航行,航行1小时后,发现此时海监船位于钓鱼岛的南偏东45°方向上的B处.
(1)求此时这艘海监船所在的B处与钓鱼岛的距离(结果保留根号)
(2)求这艘海监船的速度.(结果精确到0.1)(参考数据: ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.44)
≈2.44)
近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数 量相同.求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?