在平面直角坐标系中，曲线C1的参数方程为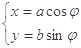
（a＞b＞0，
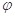为参数），以Ο为极点，x轴的正半轴为极轴建立极坐标系，曲线C2是圆心在极轴上且经过极点的圆，已知曲线C1上的点M
对应的参数
=
，
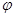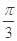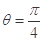与曲线C2交于点D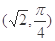
（1）求曲线C1，C2的普通方程；
（2）A（ρ1，θ），Β（ρ2，θ+
）是曲线C1上的两点，求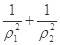
的值
（本小题满分12分）
|
已知点A是抛物线y2＝2px（p>0）上一点，F为抛物线的焦点，准线l与x轴交于点K，已知｜AK｜＝
｜AF｜，三角形AFK的面积等于8．
（本小题满分13分）如图，在矩形ABCD中，已知A（2，0）、C（－2，2），点P在BC边上移动，线段OP的垂直平分线交y轴于点E，点M满足
（Ⅰ）求点M的轨迹方程；
（Ⅱ）已知点F（0，
），过点F的直线l交点M的轨迹于Q、R两点，且
求实数
的取值范围.
（本小题满分14分）已知等比数列
的前
项和为
（Ⅰ）求数列的通项公式；
（Ⅱ）设数列
满足
，
为数列的前项和，试比较
与 
的大小，并证明你的结论．
已知向量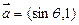
，
，
（1）若
⊥
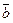, 且－
＜
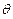＜． 求；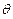
（2）求函数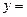
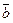|＋|的单调增区间和函数图像的对称轴方程．
求数列
的前
项和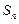
.