我市某校某数学老师这学期分别用
两种不同的教学方式试验高一甲、乙两个班（人数均为60人，入学数学平均分和优秀率都相同，勤奋程度和自觉性都一样）。现随机抽取甲、乙两班各20名的数学期末考试成绩，并作出茎叶图如下：
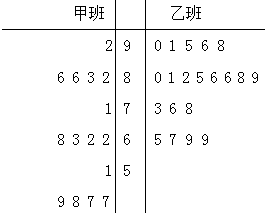
（Ⅰ）依茎叶图判断哪个班的平均分高？
（Ⅱ）现从甲班所抽数学成绩不低于80分的同学中随机抽取两名同学，用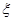
表示抽到成绩为86分的人数，求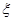的分布列和数学期望；
（Ⅲ）学校规定：成绩不低于85分的为优秀，作出分类变量成绩与教学方式的
列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”
下面临界值表仅供参考：
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
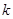2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
（参考公式：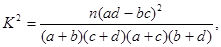
其中
）
已知定义域为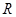
的函数
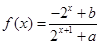是奇函数。
（Ⅰ）求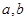
的值；
（Ⅱ）解不等式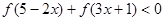
为了预防流感，某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中，室内每立方米空气中的含药量y（毫克）与时间t（小时）成正比；药物释放完毕后，y与t的函数关系式为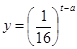
（a为常数），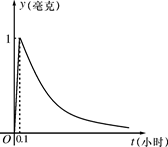
如图所示，根据图中提供的信息，回答下列问题：
（Ⅰ）从药物释放开始，求每立方米空气中的含药量
y（毫克）与时间t（小时）之间的函数关系式?
（Ⅱ）据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那从药物释放开始，至少需要经过多少小时后，学生才能回到教室.
已知函数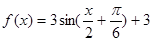
，
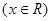
（1）用五点法画出它在一个周期内的闭区间上的图象；
（2）求单调增减区间。
已知
为第三象限角，
.
（1）化简
；
（2）若
，求的值.
（1）
；
（2）已知
，且
，求
的值。