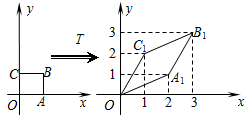
如图,单位正方形OABC在二阶矩阵T的作用下,变成菱形OA1B1C1.求矩阵T;设双曲线F:x2-y2=1在矩阵T对应的变换作用下得到曲线F´,求曲线F´的方程.
(本题小满12分)设数列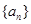 的前
的前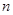 项和
项和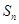 满足:
满足: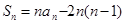 ,等比数列
,等比数列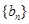 的前
的前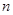 项和为
项和为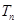 ,公比为
,公比为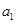 ,且
,且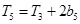 .
.
(1)求数列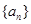 的通项公式;
的通项公式;
(2)设数列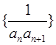 的前
的前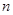 项和为
项和为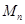 ,求证:
,求证: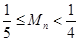 .
.
(本题小满分12分)已知数列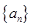 是公比大于1的等比数列,a1,a3是函数
是公比大于1的等比数列,a1,a3是函数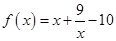 的两个零点.
的两个零点.
(1)求数列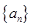 的通项公式;
的通项公式;
(2)若数列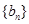 满足
满足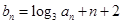 ,且
,且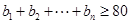 ,求
,求 的最小值.
的最小值.
(本小题满分10分)已知函数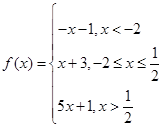
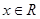 .
.
(1)求函数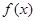 的最小值;
的最小值;
(2)已知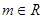 ,命题
,命题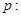 关于
关于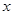 的不等式
的不等式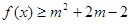 对任意
对任意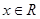 恒成立;
恒成立;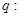 函数
函数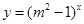 是增函数.若
是增函数.若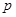 或
或 为真,
为真,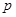 且
且 为假,求实数
为假,求实数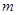 的取值范围.
的取值范围.
若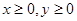 且
且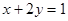 ,那么
,那么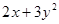 的最小值为()
的最小值为()
| A.2 | B.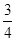 |
C.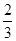 |
D. |
(本小题满分12分)设函数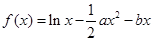 .
.
(1)当 时,求函数
时,求函数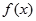 的最大值;
的最大值;
(2)令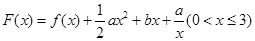 其图象上任意一点
其图象上任意一点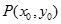 处切线的斜率
处切线的斜率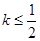 ,恒成立,求实数
,恒成立,求实数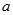 的取值范围;
的取值范围;
(3)当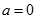 ,
,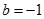 ,方程
,方程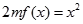 有唯一实数解,求正数
有唯一实数解,求正数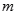 的值.
的值.