某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.
(1)从每班抽取的学生中各随机抽取一人,求至少有一人及格的概率
(2)从甲班10人中随机抽取一人,乙班10人中随机抽取两人,三人中及格人数记为X,求X的分布列和期望.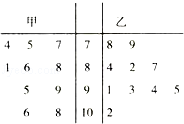
选修4—4:坐标系与参数方程
极坐标系与直角坐标系 有相同的长度单位,以原点为极点,以
有相同的长度单位,以原点为极点,以 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线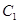 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数,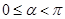 ),射线
),射线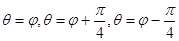 与曲线
与曲线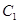 交于(不包括极点O)三点
交于(不包括极点O)三点
(1)求证: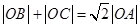 ;
;
(2)当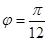 时,B,C两点在曲线
时,B,C两点在曲线 上,求
上,求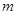 与
与 的值
的值
选修4—1:几何证明选讲
如图,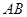 是⊙
是⊙ 的一条切线,切点为
的一条切线,切点为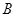 ,
, 都是⊙
都是⊙ 的割线,
的割线,

(1)证明: ;
;
(2)证明: ∥
∥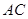 .
.
已知函数
(1)若函数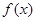 在区间
在区间 上为增函数,求
上为增函数,求 的取值范围;
的取值范围;
(2)当 且
且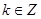 时,不等式
时,不等式 在
在 上恒成立,求
上恒成立,求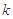 的最大值.
的最大值.
已知 其中
其中
(1)求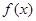 的单调区间;
的单调区间;
(2)设 ,函数
,函数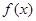 在区间
在区间 上的最大值为
上的最大值为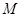 ,最小值为
,最小值为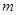 ,求
,求 的取值范围.
的取值范围.
某种产品每件成本为6元,每件售价为 元
元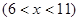 ,年销售
,年销售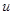 万件,已知
万件,已知 与
与 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销量利润 关于售价
关于售价 的函数关系式;
的函数关系式;
(2)求售价为多少时,年利润最大,并求出最大年利润.