(本小题满分14分)已知椭圆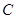 :
: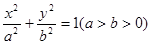 的上顶点为
的上顶点为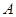 ,两个焦点为
,两个焦点为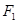 、
、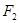 ,
,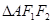 为正三角形且周长为6.
为正三角形且周长为6.
(Ⅰ)求椭圆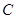 的标准方程;
的标准方程;
(Ⅱ)已知圆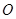 :
: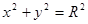 ,若直线
,若直线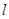 与椭圆
与椭圆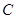 只有一个公共点
只有一个公共点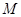 ,且直线
,且直线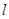 与圆
与圆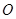 相切于点
相切于点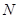 ;求
;求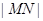 的最大值.
的最大值.
(本小题满分13分)已知函数 ,其中
,其中 为常数,且
为常数,且 .
.
(Ⅰ)若曲线 在点(1,
在点(1, )处的切线与直线
)处的切线与直线 垂直,求
垂直,求 的值;
的值;
(Ⅱ)若函数 在区间[1,2]上的最小值的表达式.
在区间[1,2]上的最小值的表达式.
(本小题满分13分)从含有两件正品和一件次品的3件产品中,每次任取1件
(Ⅰ)每次取出后不放回,连续取两次,求取出的产品中恰有一件次品的概率;
(Ⅱ)每次取出后放回,连续取两次,求取出的产品中恰有一件次品的概率.
(本小题满分14分) 如图,在四棱锥 中,底面
中,底面 为矩形,平面
为矩形,平面 平面
平面 ,
, ,
, ,
, 为
为 的中点,求证:
的中点,求证:
(Ⅰ) 平面
平面 ;
;
(Ⅱ)平面 平面
平面 ;
;
(Ⅲ)求四棱锥 的体积.
的体积.
(本小题满分13分)已知函数 ,
,
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)记 的内角A,B,C的对边长分别为
的内角A,B,C的对边长分别为 ,若
,若 ,求
,求 的值.
的值.