(本小题满分14分)
已知函数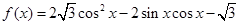 ,
,
(1) 求函数的最小正周期及取得最小值的x的集合;
(2) 求函数 的单调递增区间.
的单调递增区间.
(3)求 在
在 处的切线方程.
处的切线方程.
(本小题满分13分)已知 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时
时 ;
;
(1)求函数 的表达式;
的表达式;
(2)画出其大致图像并指出其单调区间.
(3)若函数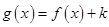 -1有三个零点,求K的取值范围;
-1有三个零点,求K的取值范围;
.设集合 ,
,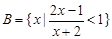 ,全集为R
,全集为R
(1)当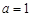 时,求:
时,求: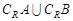 ;
;
(2)若 ,求实数
,求实数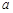 的取值范围.
的取值范围.
(3)当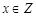 时,求B的非空真子集的个数;
时,求B的非空真子集的个数;
(本小题满分12分)
已知二次函数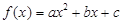 .
.
(1)若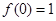 ,
,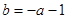 ,解关于x不等式
,解关于x不等式 ;
;
(2)若f(x)的最小值为0,且A.<b,设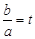 ,请把
,请把 表示成关于t的函数g(t),并求g(t)的最小值.
表示成关于t的函数g(t),并求g(t)的最小值.
(本小题满分12分)
如图1,在三棱锥P-A.BC中,PA.⊥平面A.BC,A.C⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.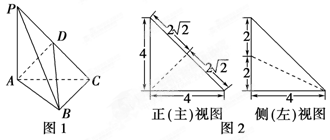
(1) 证明:A.D⊥平面PBC;
(2) 求三棱锥D-A.BC的体积;
(3) 在∠A.CB的平分线上确定一点Q,使得PQ∥平面A.BD,并求此时PQ的长.