已知圆C的圆心在坐标原点,且与直线 相切
相切
(1)求直线 被圆C所截得的弦AB的长.
被圆C所截得的弦AB的长.
(2)过点G(1,3)作两条与圆C相切的直线,切点分别为M,N求直线MN的方程
(3)若与直线l1垂直的直线l与圆C交于不同的两点P,Q,若∠POQ为钝角,求直线l纵截距的取值范围.
将一颗质地均匀的正方体骰子(六个面的点数分别为1、2、3、4、5、6)先后抛两次,将得到的点数分别记为a,b.
(1)求满足条件a+b≥9的概率;
(2)求直线ax+by+5=0与x2+y2=1相切的概率
(3)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。
已知向量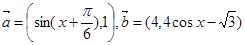
(1)若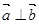 ,求
,求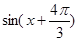 的值;
的值;
(2)设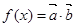 ,若
,若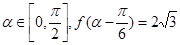 ,求
,求 的值.
的值.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm)获得身高数据如下:
| 甲班: |
158 |
168 |
162 |
168 |
163 |
170 |
182 |
179 |
171 |
179 |
| 乙班: |
159 |
168 |
162 |
170 |
165 |
173 |
176 |
181 |
178 |
179 |
(1)完成数据的茎叶图(以百位十位为茎,以个位为叶),并求甲班样本数据的中位数、众数;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
已知向量
(1)证明:
(2)若向量满足 ,且
,且 ,求
,求 .
.