抛物线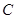 的方程为
的方程为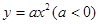 ,过抛物线
,过抛物线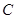 上一点
上一点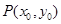 (
( )作斜率为
)作斜率为 的两条直线分别交抛物线
的两条直线分别交抛物线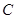 于
于 两点(
两点(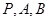 三点互不相同),且满足
三点互不相同),且满足 (
( 且
且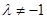 ).
).
(1)求抛物线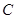 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(2)设直线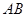 上一点
上一点 ,满足
,满足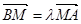 ,证明线段
,证明线段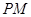 的中点在
的中点在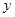 轴上;
轴上;
(3)当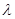 =1时,若点
=1时,若点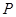 的坐标为
的坐标为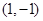 ,求
,求 为钝角时点
为钝角时点 的纵坐标
的纵坐标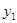 的取值范围.
的取值范围.
已知函数 (
( ).
).
(Ⅰ)若 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,
, ,总有
,总有 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数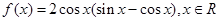 .
.
(Ⅰ)求函数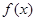 图像的对称中心;
图像的对称中心;
(Ⅱ)求函数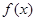 在区间
在区间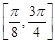 上的最小值和最大值.
上的最小值和最大值.
对于任意的 (
(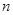 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前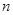 项和等于该数列的前
项和等于该数列的前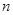 项之积,则称该数列为
项之积,则称该数列为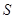 型数列。
型数列。
(1)若数列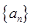 是首项
是首项 的
的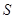 型数列,求
型数列,求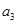 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是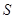 型数列;
型数列;
(3)若数列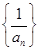 是
是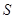 型数列,且
型数列,且 试求
试求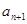 与
与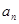 的递推关系,并证明
的递推关系,并证明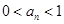 对
对 恒成立。
恒成立。
已知椭圆: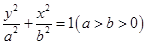 ,离心率为
,离心率为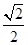 ,焦点
,焦点 过
过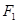 的直线交椭圆于
的直线交椭圆于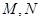 两点,且
两点,且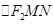 的周长为4.
的周长为4.
(Ⅰ)求椭圆方程;
(Ⅱ) 直线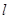 与y轴交于点P(0,m)(m
与y轴交于点P(0,m)(m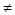 0),与椭圆C交于相异两点A,B且
0),与椭圆C交于相异两点A,B且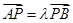 .若
.若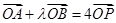 ,求m的取值范围。
,求m的取值范围。
(理)已知函数f(x)=  -lnx,x∈[1,3].
-lnx,x∈[1,3].
(Ⅰ)求f(x)的最大值与最小值;
(Ⅱ)若f(x)<4-At对于任意的x∈[1,3],t∈[0,2]恒成立,求实数A的取值范围.