如图,在四棱锥 中,四边形
中,四边形 是平行四边形,
是平行四边形,
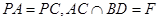 ,点E是
,点E是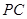 的中点.
的中点.
(1)求证: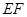 ∥平面
∥平面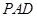 ;
;
(2)求证:平面 平面
平面 .
.
已知两点 ,
, .
.
(1)求过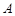 、
、 两点的直线方程;
两点的直线方程;
(2)求线段 的垂直平分线
的垂直平分线 的直线方程;
的直线方程;
(3)若圆 经过
经过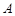 、
、 两点且圆心在直线
两点且圆心在直线 上,求圆
上,求圆 的方程.
的方程.
已知函数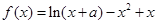 ,
,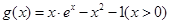 ,且
,且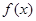 点
点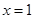 处取得极值.
处取得极值.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若关于 的方程
的方程 在区间
在区间 上有解,求
上有解,求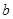 的取值范围;
的取值范围;
(Ⅲ)证明: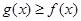 .
.
已知椭圆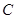 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆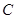 右焦点
右焦点 ,且
,且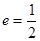
(1)求椭圆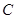 的标准方程;
的标准方程;
(2)若直线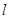 :
: 与椭圆
与椭圆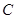 相交于
相交于 ,
,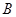 两点(
两点( 都不是顶点),且以
都不是顶点),且以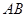 为直径
为直径
的圆过椭圆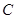 的右顶点,求证:直线
的右顶点,求证:直线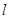 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
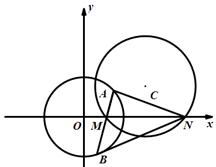
如图,圆 :
: .
.
(Ⅰ)若圆 与
与 轴相切,求圆
轴相切,求圆 的方程;
的方程;
(Ⅱ)已知 ,圆
,圆 与
与 轴相交于两点
轴相交于两点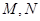 (点
(点 在点
在点 的左侧).过点
的左侧).过点 任作一条直线与圆
任作一条直线与圆 :
: 相交于两点
相交于两点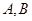 .问:是否存在实数
.问:是否存在实数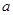 ,使得
,使得 ?若存在,求出实数
?若存在,求出实数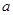 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.