已知椭圆C: 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 与以椭圆C的右焦点为圆心,以
与以椭圆C的右焦点为圆心,以
 为半径的圆相切.
为半径的圆相切.
(1)求椭圆的方程.
(2)若过椭圆 的右焦点
的右焦点 作直线
作直线 交椭圆
交椭圆 于
于 两点,交y轴于
两点,交y轴于 点,且
点,且 求证:
求证: 为定值
为定值
已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)="T" f(x)成立.
(Ⅰ)函数f(x)=" x" 是否属于集合M?说明理由;
(Ⅱ)设函数f(x)=ax(a>0,且a≠1)的图象与y=x的图象有公共点,证明:f(x)=ax∈M;
(Ⅲ)若函数f(x)=sinkx∈M ,求实数k的值.
已知 ,
, ,其中
,其中 是自然常数).
是自然常数).
(Ⅰ)求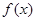 的单调性和极小值;
的单调性和极小值;
(Ⅱ)求证: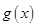 在
在 上单调递增;
上单调递增;
(Ⅲ)求证: .
.
已知数列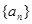 满足递推式
满足递推式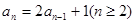 ,其中
,其中
(Ⅰ)求 ;
;
(Ⅱ) 并求数列
并求数列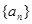 的通项公式;
的通项公式;
(Ⅲ)已知数列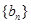 有
有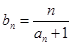 求数列
求数列 的前n项和
的前n项和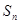 .
.
在 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,且满足
,且满足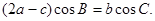
(Ⅰ)求角B的大小;
(Ⅱ)若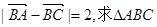 的面积的最大值.
的面积的最大值.
在△ABC中,角A,B,C所对的边分别为a,b,c,设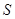 为△ABC的面积,满足
为△ABC的面积,满足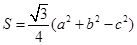 .(1)求角C的大小;(2)求
.(1)求角C的大小;(2)求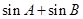 的最大值.
的最大值.