如图，抛物线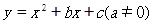
与x轴交于A（1，0）、B（-4，0）两点。
（1）求该抛物线的解析式；
（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．
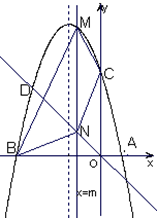
（3）设此抛物线与直线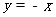
在第二象限交于点D，平行于
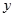轴的直线
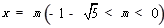与抛物线交于点M，与直线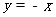交于点N，连接BM、CM、NC、NB，是否存在
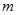的值，使四边形BNCM的面积S最大？若存在，请求出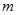的值，若不存在，请说明理由．
如图，⊙O是△ABC的外接圆，FH是⊙O 的切线，切点为F，
FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．
（1）证明：AF平分∠BAC；
（2）证明：BF＝FD；
（3）若EF＝4，DE＝3，求AD的长．
某校初三年级春游，现有36座和42座两种客车供选择租用，若只租用36座客车若干辆，则正好坐满；若只租用42座客车，则能少租一辆，且有一辆车没有坐满，但超过30人；已知36座客车每辆租金400元，42座客车每辆租金440元.
（1）该校初三年级共有多少人参加春游？
（2）请你帮该校设计一种最省钱的租车方案．
某蔬菜公司收购到某种蔬菜104吨，准备加工后上市销售. 该公司加工该种蔬菜的能力是：每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务，则该公司应安排几天精加工，几天粗加工？
如图是某地6月1日至6月7日每天最高、最低气温的折线统计图．
请你根据折线统计图，回答下列问题：
(1)在这7天中，日温差最大的一天是6月_____日；
(2)这7天的日最高气温的平均数是______℃；
(3)这7天日最高气温的方差是 _______．
求证：矩形的对角线相等．