在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出1个小球,每个小球被取出的可能性相等.
(1)求取出的两个球上的编号都为奇数的概率;
(2)求取出的两个球上的编号之和为3的倍数的概率;
(3)求取出的两个球上的编号之和大于6的概率.
(本小题满分12分)
函数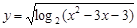 的定义域为集合
的定义域为集合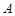 ,
,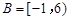 ,
,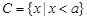 .
.
(Ⅰ)求集合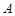 及
及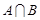 ;
;
(Ⅱ)若 ,求
,求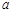 的取值范围.
的取值范围.
(本小题满分12分)
如图,已知点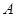 是椭圆
是椭圆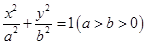 的右顶点,若点
的右顶点,若点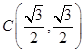 在椭圆上,且满足
在椭圆上,且满足 .(其中
.(其中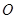 为坐标原点)
为坐标原点)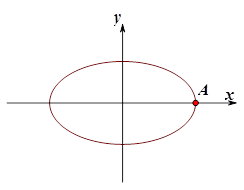
(1)求椭圆的方程;
(2)若直线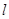 与椭圆交于两点
与椭圆交于两点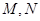 ,当
,当 时,求
时,求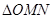 面积的最大值.
面积的最大值.
(本小题满分12分)
在如图所示的四棱锥 中,已知 PA⊥平面ABCD,
中,已知 PA⊥平面ABCD,  ,
,  ,
, ,
, 为
为 的中点.
的中点.
(1)求证:MC∥平面PAD;
(2)求直线MC与平面PAC所成角的余弦值;
(3)求二面角 的平面角的正切值.
的平面角的正切值.
(本小题满分12分)
如图椭圆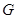 :
:
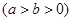 的两个焦点为
的两个焦点为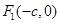 、
、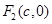 和顶点
和顶点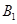 、
、 构成面积为32的正方形.
构成面积为32的正方形.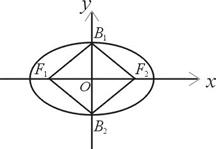
(1)求此时椭圆 的方程;
的方程;
(2)设斜率为 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 、
、 、
、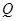 为
为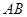 的中点,且
的中点,且 . 问:
. 问: 、
、 两点能否关于直线
两点能否关于直线 对称. 若能,求出
对称. 若能,求出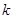 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
(本小题满分12分)
设双曲线 的方程为
的方程为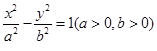 ,
,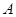 、
、 为其左、右两个顶点,
为其左、右两个顶点,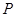 是双曲线
是双曲线 上的任意一点,作
上的任意一点,作 ,
,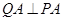 ,垂足分别为
,垂足分别为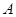 、
、 ,
, 与
与 交于点
交于点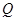 .
.
(1)求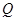 点的轨迹
点的轨迹 方程;
方程;
(2)设 、
、 的离心率分别为
的离心率分别为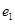 、
、 ,当
,当 时,求
时,求 的取值范围.
的取值范围.