某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。 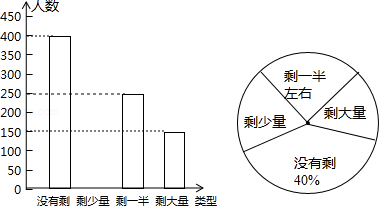
(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
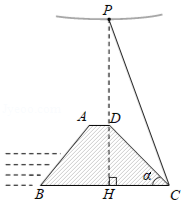
沿江大堤经过改造后的某处横断面为如图所示的梯形 ,高 米,斜坡 的坡度 .此处大堤的正上方有高压电线穿过, 表示高压线上的点与堤面 的最近距离 、 、 在同一直线上),在点 处测得 .
(1)求斜坡 的坡角 ;
(2)电力部门要求此处高压线离堤面 的安全距离不低于18米,请问此次改造是否符合电力部门的安全要求?
(参考数据: , , ,
为了了解现行简化汉字的笔画画数情况,某同学随机选取语文课本的一篇文章,对其部分文字的笔画数进行统计,结果如下表:
|
笔画数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
字数 |
4 |
8 |
10 |
16 |
14 |
20 |
24 |
36 |
16 |
14 |
11 |
9 |
10 |
7 |
1 |
请答案下列问题:
(1)被统计汉字笔画数的众数是多少?
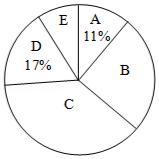
(2)该同学将数据进行整理,按如下方案分组统计,并制作扇形统计图:
|
分组 |
笔画数 (画 |
字数(个 |
|
组 |
|
22 |
|
组 |
|
|
|
组 |
|
76 |
|
组 |
|
|
|
组 |
|
18 |
请确定上表中的 、 的值及扇形统计图中 组对应扇形圆心角的度数;
(3)若这篇文章共有3500个汉字,估计笔画数在 画 组)的字数有多少个?
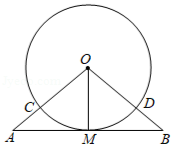
如图, 是 的半径,过 点作 的切线 ,且 , , 分别交 于 , .求证: .
先化简,再求值: ,其中 .
计算: .