某商场为了吸引顾客规定，凡购买200元以上物品的顾客均可获奖，可以直接获得购物券10元，也可以参加摸奖．摸奖的具体方法是：从一个装有100个彩球的盒子中任取一球，摸到红球可获100元的购物券，摸到黄球可获50元的购物券，摸到蓝球可获加元的购物券，而摸到白球则不能获奖．已知100个球中，5个红球，10个黄球，20个蓝球，其余均为白球．小明购买200元以上物品，但是没有立刻抽奖．为了弄明白自己获奖的机会的大小，特别在摸奖台旁边观察，下面图表就是小明观察的结果：
问：（1）小明共观察统计了多少顾客?
（2）小明画的条形统计图不完整，请补充完整；
（3）在扇形统计图中，“摸蓝球”所在的扇形圆心角为多少度?
（4）小明经过观察和比较，选择了比较合算的方式．请说明他是直接拿购物券10元，还是参加了摸奖呢?
如图，AC是⊙O的直径，PB切⊙O于点D，交AC的延长线于点B，且∠DAB＝∠B．
（1）求∠B的度数；
（2）若BD＝9，求BC的长．
如图，在矩形ABCD中， CF⊥BD分别交BD、AD于点E、F．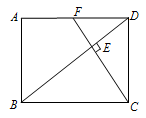
（1）求证：△DEC ∽ △FDC；
（2）若DE＝2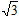
，F为AD的中点，求BD的长度．
（1）如图①，用尺规作图作出圆的一条直径EF（不写作法,保留作图痕迹）；
（2）如图②，A、B、C、D为圆上四点，AB∥CD，AB＜CD，请只用无刻度的直尺，画出圆的一条直径EF（不写画法，保留画图痕迹）．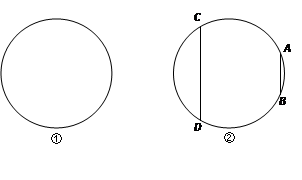
关于x的一元二次方程（a＋c）x2＋2bx＋（a－c）＝0，其中a、b、c分别为△ABC三边的长．
（1）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（2）如果△ABC是等边三角形，试求这个一元二次方程的根．
（1）问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．求证：AD·BC=AP·BP．
（2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．
（3）应用：请利用（1）（2）获得的经验解决问题：
如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当DC的长与△ABD底边上的高相等时，求t的值．