已知直线 :
: ,
,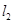 :
: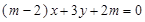 ,求当
,求当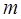 为何值时,
为何值时, 与
与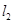 :(1)平行;(2)相交;(3)垂直.
:(1)平行;(2)相交;(3)垂直.
将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(I)共有多少种不同的结果?
(II)两枚骰子点数之和是3的倍数的结果有多少种?
(III)两枚骰子点数之和是3的倍数的概率是多少?
(本小题满分10分)如图,在 中,
中, ,以
,以 为直径的圆
为直径的圆 交
交 于点
于点 ,连接
,连接 ,并延长交
,并延长交 的延长线于点
的延长线于点 ,圆
,圆 的切线
的切线 交
交 于
于
(Ⅰ)证明: ;
;
(Ⅱ)若 ,
, ,求
,求 的长。
的长。
(本小题满分10分)函数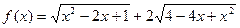 .
.
(Ⅰ)求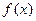 的值域;
的值域;
(Ⅱ)关于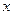 的不等式
的不等式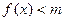 有解,求实数
有解,求实数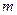 的范围.
的范围.
(本小题满分10分)已知曲线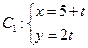 (
(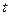 为参数),
为参数),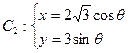 (
(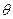 为参数),点
为参数),点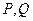 分别在曲线
分别在曲线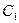 和
和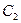 上,求线段
上,求线段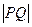 长度的最小值.
长度的最小值.
(本小题满分12分)已知函数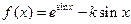 .
.
(Ⅰ)若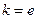 ,试确定函数
,试确定函数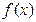 的单调递增区间;
的单调递增区间;
(Ⅱ)若对于任意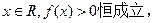 试确定实数
试确定实数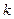 的取值范围;
的取值范围;
(Ⅲ)若函数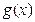 =
=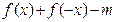 在
在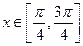 上有两个零点,求实数
上有两个零点,求实数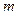 的取值范围.
的取值范围.