(本小题满分10分)选修4-1:几何证明选讲
如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F.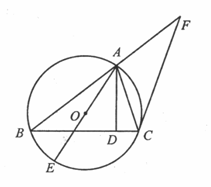
(Ⅰ)求证:AC·BC="AD·AE;"
(Ⅱ)若AF="2," CF=2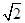 ,求AE的长
,求AE的长
如图,已知AF 平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,
平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形, DAB
DAB ,AB//CD,AD
,AB//CD,AD AF
AF CD
CD 2,AB
2,AB 4.
4. 
(Ⅰ)求证:AC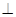 平面BCE;
平面BCE;
(Ⅱ)求三棱锥A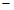 CDE的体积;
CDE的体积;
(Ⅲ)线段EF上是否存在一点M,使得BM CE ?若存在,确定M点的位置;若不存在,请说明理由.
CE ?若存在,确定M点的位置;若不存在,请说明理由.
已知数列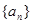 的前
的前 项和为
项和为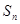 ,且
,且 (其中
(其中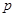 是不为零的常数),
是不为零的常数), .
.
(Ⅰ)证明:数列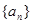 是等比数列;
是等比数列;
(Ⅱ)当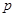 =1时,数列
=1时,数列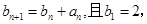 求数列
求数列 的通项公式.
的通项公式.
在 中,角
中,角 所对的三边分别为
所对的三边分别为 ,
, ,且
,且
(Ⅰ)求 ;
;
(Ⅱ)求 的面积.
的面积.
已知函数 .
.
(Ⅰ)若曲线 在点(0,1)处切线的斜率为-3,求函数
在点(0,1)处切线的斜率为-3,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 在区间[-2,
在区间[-2, ]上单调递增,求
]上单调递增,求 的取值范围.
的取值范围.
已知椭圆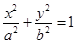
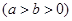 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为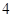 ,且过点
,且过点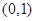 .
.
(Ⅰ)求椭圆方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为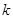 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点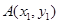 ,
,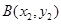 ,若
,若 ,求△
,求△ 的面积.
的面积.