已知椭圆E: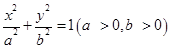 的离心率
的离心率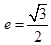 ,并且经过定点
,并且经过定点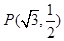
(1)求椭圆E 的方程;
(2)问是否存在直线y=-x+m,使直线与椭圆交于A, B 两点,满足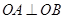 ,若存在求m 值,若不存在说明理由.
,若存在求m 值,若不存在说明理由.
(本小题满分12分)
已知数列 的前
的前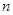 项和为
项和为 满足:
满足: (
( 为常数,且
为常数,且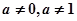 )
)
(1)若 ,求数列
,求数列 的通项公式
的通项公式
(2)设 ,若数列
,若数列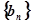 为等比数列,求
为等比数列,求 的值.
的值.
(3)在满足条件(2)的情形下,设 ,数列
,数列 前
前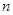 项和为
项和为 ,求证
,求证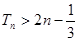
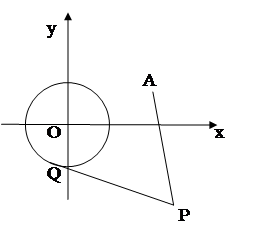
(本小题满分12分)已知圆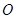 :
: 和定点
和定点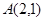 ,由圆外一点
,由圆外一点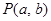 向圆
向圆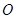 引切线
引切线 ,切点为
,切点为 ,且满足
,且满足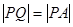 .
.
(1)求实数 间满足的等量关系式;
间满足的等量关系式;
(2)求 面积的最小值;
面积的最小值;
(3)求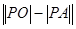 的最大值。
的最大值。
(本小题满分12分)
已知椭圆 的离心率
的离心率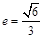 ,过点
,过点 和
和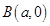 的直线与原点的距离为
的直线与原点的距离为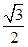 。⑴求椭圆的方程;⑵已知定点
。⑴求椭圆的方程;⑵已知定点 ,若直线
,若直线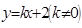 与椭圆交于
与椭圆交于 两点,问:是否存在
两点,问:是否存在 的值,使以
的值,使以 为直径的圆过
为直径的圆过 点?请说明理由。
点?请说明理由。
(本小题满分12分)一个四棱锥的直观图和三视图如图所示: 

(1)求证: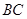 ⊥
⊥ ;
;
(2)求出这个几何体的体积。
(3)若在PC上有一点E,满足CE:EP=2:1,求证PA//平面BED。
已知直线 与圆
与圆 的交点为A、B,
的交点为A、B,
(1)求弦长AB;
(2)求过A、B两点且面积最小的圆的方程.