如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN．
（1）求证：四边形AMDN是平行四边形．
（2）当AM的值为何值时，四边形AMDN是矩形？请说明理由．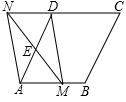
观察等式：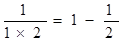
，
，
，
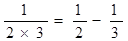将以上三个等式两边分别相加得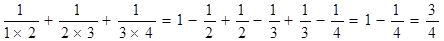
.
（1）猜想并写出：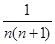
=____________________.
（2）直接写出下式的计算结果：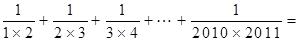
__________________________.
（3）探究并计算：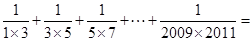
______________________.
某市出租车收费标准为：起步价7元（即行驶距离不超过3km,都付7元车费），超过3km后，每增加1km，加收2.2元（不足1km,按1km计算）。某人乘坐了xkm（x为大于3的整数）路程。
（1）试用代数式表示他应付的车费；
（2）求当x=8km时的乘车费用；
（3）若此人付了29元车费，你能计算出此人乘坐的最远路程吗？
国庆前夕，新昌县质量技术监督局对该县某企业生产的罐头进行了抽检，从库中任意抽出样品20听进行检测，每听的质量超过标准质量部分记为正，不足部分记为负，记录如下表：
| 与标准质量的差（克） |
-8 |
-5 |
0 |
+2 |
+10 |
+12 |
| 听数 |
2 |
1 |
5 |
6 |
4 |
2 |
问这批样品平均每听质量比标准每听质量多或少几克？
．分解因式：a5－a3b2＋ab4
已知方程|2a＋3b＋1|＋（3a－b－1）2＝0，求a2＋2ab＋b2的值.