已知等差数列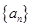 的首项
的首项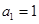 ,公差
,公差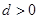 ,且其第二项、第五项、第十四项分别是等比数列
,且其第二项、第五项、第十四项分别是等比数列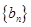 的第二、三、四项.
的第二、三、四项.
(1)求数列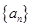 与
与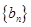 的通项公式;
的通项公式;
(2)令数列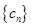 满足:
满足: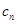 =
= ,求数列
,求数列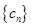 的前101项之和
的前101项之和 ;
;
(3)设数列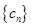 对任意
对任意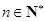 ,均有
,均有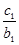 +
+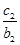 + +
+ +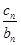 =
= 成立,求
成立,求 的值.
的值.
(本小题满分12分)如图,在三棱柱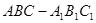 中,
中,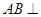 侧面
侧面 ,已知
,已知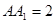 ,
,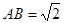 ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)当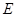 点为棱
点为棱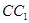 的中点时,求
的中点时,求 与平面
与平面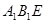 所成的角的正弦值.
所成的角的正弦值.
(本小题满分12分)已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图所示,从这10名学生中随机抽取两名成绩不低于73分的学生, 求被抽取到的两名学生的成绩之和不小于154分的概率.
(本小题满分12分)已知 且
且 .设函数
.设函数
(1)求函数 的解析式;
的解析式;
(2)若在锐角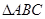 中,
中, ,边
,边 ,求
,求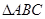 周长的最大值.
周长的最大值.
(本小题满分13分) 已知函数 (
( ).
).
(1)求函数 的单调区间;
的单调区间;
(2)函数 在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
(3)若 ,当
,当 时,不等式
时,不等式 恒成立,求α的取值范围.
恒成立,求α的取值范围.
(本小题满分13分)已知 分另为椭圆的上、下焦点,
分另为椭圆的上、下焦点, 是抛物线
是抛物线 的焦点,点
的焦点,点 是
是 与
与 在第二象限的交点, 且
在第二象限的交点, 且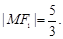
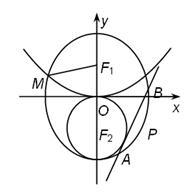
(1)求椭圆 的方程;
的方程;
(2)与圆 相切的直线
相切的直线 交椭圆
交椭圆 于
于 ,若椭圆
,若椭圆 上一点
上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.