列{an}的前n项和为Sn,已知Sn+1=pSn+q(p,q为常数,n∈N*),a1=2,a2=1,a3=q-3p.
(1)求p,q的值;
(2)求数列{an}的通项公式;
(3)是否存在正整数m,n,使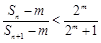 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由.
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由.
在四面体 中, , ,且 分别是 的中点,
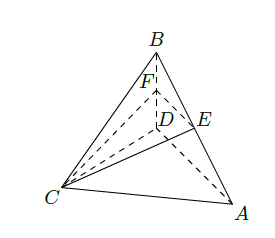
求证:
(I)直线
;
(II)
。
如图,在平面直角坐标系 中,以 轴为始边做两个锐角 ,它们的终边分别与单位圆相交于 两点,已知 的横坐标分别为 .
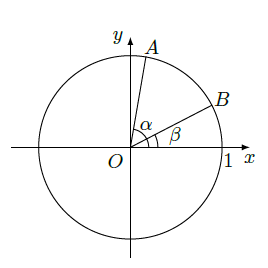
(1)求 的值;
(2)求 的值.
设椭圆 的左右焦点分别为 ,离心率 ,右准线为 是 上的两个动点, 。
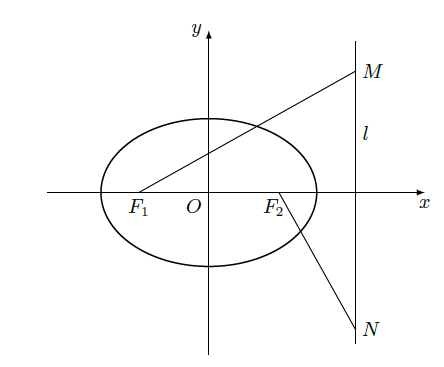
(Ⅰ)若
,求
的值;
(Ⅱ)证明:当
取最小值时,
与
共线。
如图,平面
平面
,四边形
与
都是直角梯形,
,
,
。
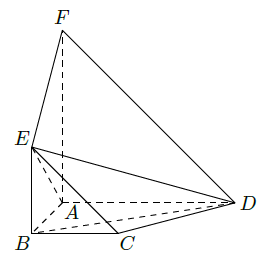
(Ⅰ)证明:
四点共面;
(Ⅱ)设
,求二面角
的大小。
设进入某商场的每一位顾客购买甲种商品的概率为
,购买乙种商品的概率为
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
的分布列及期望。
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
的分布列及期望。