在△ 中,
中, ,
, ,
,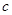 分别是△
分别是△ 内角
内角 ,
,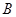 ,
,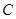 的对边,
的对边, .
.
(1)求角 的值;
的值;
(2)已知 =2,求3(
=2,求3( +
+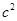 )的取值范围.
)的取值范围.
向量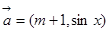 ,
,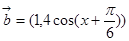 ,设函数
,设函数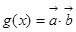 ,(
,( ,且
,且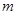 为常数)
为常数)
(1)若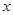 为任意实数,求
为任意实数,求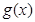 的最小正周期;
的最小正周期;
(2)若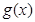 在
在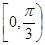 上的最大值与最小值之和为
上的最大值与最小值之和为 ,求
,求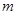 的值.
的值.
(本小题满分15分)已知函数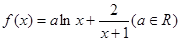 .
.
(1)当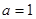 时,求
时,求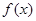 在
在 最小值;
最小值;
(2)若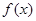 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(3)求证: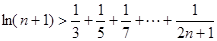 (
( ).
).
(本小题满分14分)已知数列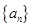 的前
的前 项和
项和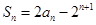 .
.
(1)证明:数列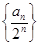 是等差数列;
是等差数列;
(2)若不等式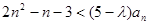 对
对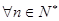 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知两个不共线的向量 ,它们的夹角为
,它们的夹角为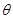 ,且
,且 ,
,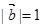 ,
,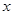 为正实数.
为正实数.
(1)若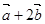 与
与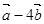 垂直,求
垂直,求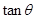 ;
;
(2)若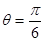 ,求
,求 的最小值及对应的
的最小值及对应的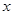 的值,并判断此时向量
的值,并判断此时向量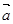 与
与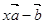 是否垂直?
是否垂直?
已知函数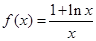 .
.
(1)若函数 在区间
在区间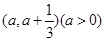 上存在极值点,求实数
上存在极值点,求实数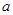 的取值范围;
的取值范围;
(2)当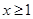 时,不等式
时,不等式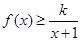 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求证: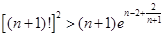 .(
.(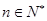 ,
, 为自然对数的底数)
为自然对数的底数)