如图是建筑工地上常用的一种“深穴打夯机”,电动机带动两个滚轮匀速转动将夯杆从深坑提上来,当夯杆底端刚到达坑口时,两个滚轮彼此分开,将夯杆释放,夯杆在自身重力作用下,落回深坑,夯实坑底,然后两个滚轮再次压紧,夯杆被提上来,如此周而复始。已知两个滚轮边缘的线速度恒为v=4m/s,滚轮对夯杆的正压力FN=2×104N,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆的质量m=1×103kg,坑深h=6.4m,假设在打夯的过程中坑的深度变化不大,取g="10" m/s2.求: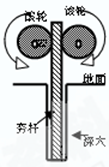
(1)每个打夯周期中,电动机对夯杆所做的功;
(2)每个打夯周期中,滚轮与夯杆间因摩擦产生的热量;
(3)打夯周期。
如图所示,某货场而将质量为m1="100" kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物中轨道顶端无初速滑下,轨道半径R="1.8" m。地面上紧靠轨道次排放两声完全相同的木板A、B,长度均为l=2m,质量均为m2="100" kg,木板上表面与轨道末端相切。货物与木板间的动摩擦因数为 1,木板与地面间的动摩擦因数
1,木板与地面间的动摩擦因数 =0.2。(最大静摩擦力与滑动摩擦力大小相等,取g="10" m/s2)
=0.2。(最大静摩擦力与滑动摩擦力大小相等,取g="10" m/s2)
求货物到达圆轨道末端时对轨道的压力。
若货物滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求
 1应满足的条件。
1应满足的条件。
“蹦极”是冒险者的运动,质量为50kg的运动员,在一座高桥上做“蹦极”运动,他所用的弹性绳自由长度为12m,假设弹性绳中的弹力与弹性绳的伸长之间的关系符合胡克定律,在整个运动中弹性绳不超过弹性限度,运动员从桥面下落,能达到距桥面为36m的最低点D处,运动员下落速度v与下落距离s的关系如图所示,运动员在C点时速度最大,空气阻力不计,重力加速度g取10m/s2,求: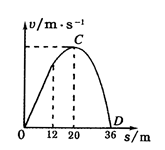
弹性绳的劲度系数k;
运动员到达D点时的加速度a的大小;
运动员到达D点时,弹性绳的弹性势能EP。
传送带被广泛地应用于码头、机场和车站,如图所示为一水平传送带的装置示意图,紧绷的传送带AB始终保持恒定的速率V=1m/s运行.将一质量m=4kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带之间的动摩擦因数μ=0.1,A、B间的距离L=2m,g取10m/s2.行李做匀加速直线运动的位移为多少?
将该行李从A端传送到B端,传送带消耗的电能?
如果提高传送带的运行速率,行李就能被较快地传送到B处,求行李从A处以最短时间传送到B处时传送带对应的最小运行速率.
如图所示,质量为m=10kg的两个相同的物块A、B(它们之间用轻绳相连)放在水平地面上,在方向与水平方面成 角斜向上、大小为100N的拉力F作用下,以大小为
角斜向上、大小为100N的拉力F作用下,以大小为 =4.0m/s的速度向右做匀速直线运动。( g=10m/s2,sin37
=4.0m/s的速度向右做匀速直线运动。( g=10m/s2,sin37 =0.6,cos37
=0.6,cos37 =0.8)
=0.8)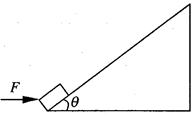
求当A、B一起匀速运动时 A、B所受的滑动摩擦力fA 、fB
若将轻绳剪断,则剪断轻绳后物块A在水平地面上滑行的距离。
如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.A点离水平地面的高度为20m.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:(g =10m/s2)
| 位置 |
A |
B |
C |
| 速度(m/s) |
2.0 |
12.0 |
0 |
| 时刻(s) |
0 |
4 |
10 |
人与雪橇从A到B的过程中,损失的机械能为多少?
设人与雪橇在BC段所受阻力恒定,求阻力大小