(本小题满分12分)设向量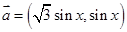 ,
, ,
,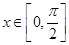 .
.
(1)若 ,求
,求 的值;
的值;
(2)设函数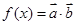 ,求
,求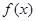 的最大值.
的最大值.
如图,已知菱形 所在平面与直角梯形
所在平面与直角梯形 所在平面互相垂直,
所在平面互相垂直,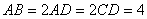 ,
,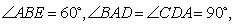 点
点 ,
,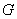 分别是线段
分别是线段 ,
, 的中点.
的中点. 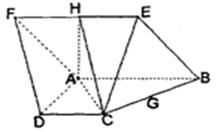
(I)求证:平面
 平面
平面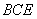 ;
;
(Ⅱ)点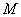 在直线
在直线 上,且
上,且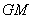 //平面
//平面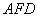 ,求平面
,求平面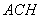 与平面
与平面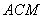 所成角的余弦值。
所成角的余弦值。
不透明的袋中有8张大小和形状完全相同的卡片,卡片上分别写有1,1,2,2,3,3,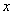 ,
,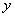 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
(I)求取出的三张卡片中至少有一张字母卡片的概率;
(Ⅱ)设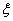 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时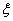 为这二个数字之和,否则
为这二个数字之和,否则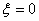 ,求
,求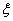 的分布列和期望
的分布列和期望 .
.
已知等差数列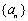 前三项的和为
前三项的和为 ,前三项的积为
,前三项的积为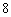 .
.
(Ⅰ)求等差数列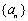 的通项公式;
的通项公式;
(Ⅱ)若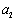 ,
,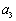 ,
,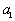 成等比数列,求数列
成等比数列,求数列 的前
的前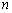 项和.
项和.
已知函数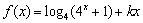 (
( )是偶函数
)是偶函数
(1)求 的值;
的值;
(2)设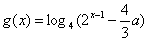 ,若函数
,若函数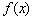 与
与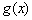 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数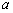 的取值范围
的取值范围
在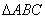 中,角
中,角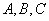 的对边分别为
的对边分别为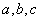 ,若
,若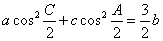 .
.
(Ⅰ)求证: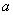 、
、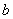 、
、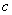 成等差数列;
成等差数列;
(Ⅱ)若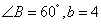 ,求
,求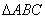 的面积.
的面积.