已知椭圆C1: +
+ =1(0<a<
=1(0<a< ,0<b<2)与椭圆C2:
,0<b<2)与椭圆C2: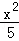 +
+ =1有相同的焦点.直线L:y=k(x+1)与两个椭圆的四个交点,自上而下顺次记为A、B、C、D.
=1有相同的焦点.直线L:y=k(x+1)与两个椭圆的四个交点,自上而下顺次记为A、B、C、D.
(Ⅰ)求线段BC的长(用k和a表示);
(Ⅱ)是否存在这样的直线L,使线段AB、BC、CD的长按此顺序构成一个等差数列.请说明详细的理由.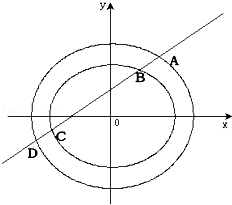
四棱锥 的底面为正方形,
的底面为正方形, 底面
底面 ,
, ,
, 为
为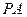 上的点.
上的点.
(1)求证:无论点 在
在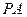 上如何移动,都有
上如何移动,都有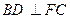 ;
;
(2)若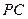 //平面
//平面 ,求二面角
,求二面角 的余弦值.
的余弦值.
已知定点A(-2,-4),过点A作倾斜角为45 的直线l,交抛物线y2=2px(p>0)于B、C两点,且|BC|=210.(Ⅰ)求抛物线的方程;(Ⅱ)在(Ⅰ)中的抛物线上是否存在点D,使得|DB|=|DC|成立?如果存在,求出点D的坐标;如果不存在,请说明理由.
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是,且面试是否合格互不影响.求:(Ⅰ)至少有1人面试合格的概率;(Ⅱ)签约人数 的分布列和数学期望.
的分布列和数学期望.
某工厂为了保障安全生产,每月初组织工人参加一次技能测试. 甲、乙两名工人通过每次测试的概率分别是和.假设两人参加测试是否通过相互之间没有影响.(Ⅰ)求甲工人连续3个月参加技能测试至少1次未通过的概率;(Ⅱ)求甲、乙两人各连续3个月参加技能测试,甲工人恰好通过2次且乙工人恰好通过1次的概率;(Ⅲ)工厂规定:工人连续2次没通过测试,则被撤销上岗资格. 求乙工人恰好参加4次测试后被撤销上岗资格的概率.
某工厂在试验阶段大量生产一种零件.这种零件有A、B两项技术指标需要检测,设各项技术指标达标与否互不影响。若有且仅有一项技术指标达标的概率为,至少一项技术指标达标的概率为.按质量检验规定:两项技术指标都达标的零件为合格品.(Ⅰ)求一个零件经过检测为合格品的概率是多少?(Ⅱ)任意依次抽出5个零件进行检测,求其中至多3个零件是合格品的概率是多少?
(Ⅲ)任意依次抽取该种零件4个,设ξ表示其中合格品的个数,求Eξ与Dξ.