(满分12分)已知一圆与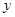 轴相切,圆心在直线
轴相切,圆心在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为 ,求该圆的方程
,求该圆的方程
如图,三棱柱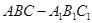 中,侧面
中,侧面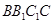 为菱形,
为菱形,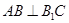 .
.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,
,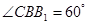 ,
,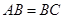 ,求二面角
,求二面角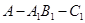 的余弦值.
的余弦值.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图: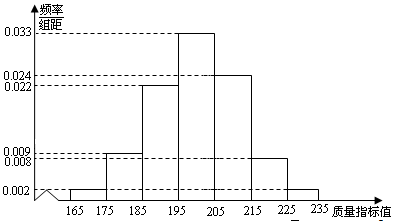
(Ⅰ)求这500件产品质量指标值的样本平均值 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表);
(Ⅱ)由直方图可以认为,这种产品的质量指标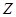 服从正态分布
服从正态分布 ,其中
,其中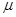 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .
.
(ⅰ)利用该正态分布,求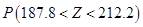 ;
;
(ⅱ)某用户从该企业购买了100件这种产品,记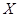 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间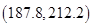 的产品件数.利用(ⅰ)的结果,求
的产品件数.利用(ⅰ)的结果,求 .
.
附: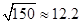 若
若 则
则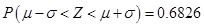 ,
,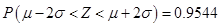 .
.
已知数列 的前
的前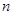 项和为
项和为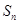 ,
,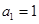 ,
, ,
,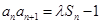 ,其中
,其中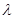 为常数.
为常数.
(1)证明: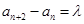 ;
;
(2)是否存在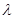 ,使得
,使得 为等差数列?并说明理由.
为等差数列?并说明理由.
如图,在△ABC中,∠ABC=90°,AB= ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
已知抛物线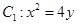 的焦点
的焦点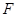 也是椭圆
也是椭圆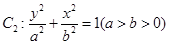 的一个焦点,
的一个焦点,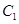 与
与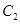 的公共弦的长为
的公共弦的长为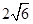 .
.
(1)求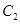 的方程;
的方程;
(2)过点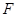 的直线
的直线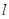 与
与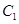 相交于
相交于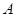 ,
,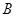 两点,与
两点,与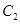 相交于
相交于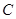 ,
,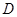 两点,且
两点,且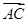 与
与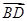 同向.
同向.
(ⅰ)若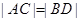 ,求直线
,求直线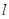 的斜率;
的斜率;
(ⅱ)设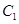 在点
在点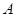 处的切线与
处的切线与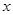 轴的交点为
轴的交点为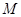 ,证明:直线
,证明:直线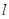 绕点
绕点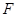 旋转时,
旋转时,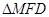 总是钝角三角形.
总是钝角三角形.