已知椭圆C:
 过点
过点 ,且离心率为
,且离心率为 .
.
(1)求椭圆的标准方程;
(2)过右焦点的直线 与椭圆
与椭圆 相交于
相交于 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程.
已知椭圆C: 的离心率为
的离心率为 ,B,F分别是它的上顶点和右焦点.椭圆C上的点到点F的最短距离为2.圆M是过点B,F的所有圆中面积最小的圆.
,B,F分别是它的上顶点和右焦点.椭圆C上的点到点F的最短距离为2.圆M是过点B,F的所有圆中面积最小的圆.
(1)求椭圆C和圆M的方程;
(2)从圆外一点P引圆M的切线PQ,切点为Q,且有|PQ|=|PO|,O是坐标原点,求|PF|的最小值.
(本小题满分14分)

某校从参加高一年级期中考试的学生中随机抽取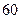 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为 的学生中抽取一个容量为
的学生中抽取一个容量为 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取 人,求至多有
人,求至多有 人在分数段
人在分数段 的概率.
的概率.
(本小题满分14分)
已知命题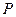 :函数
:函数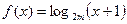 是增函数;命题
是增函数;命题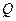 :
: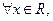
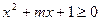 .
.
(1)写出命题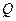 的否命题
的否命题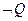 ;并求出实数
;并求出实数 的取值范围,使得命题
的取值范围,使得命题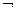
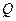 为真命题;
为真命题;
(2)如果“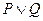 ” 为真命题,“
” 为真命题,“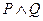 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知四棱锥 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.
(1)求证:
(2)若五点 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
 |
|||
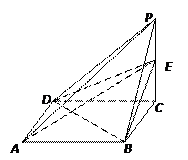 |
|||
(本小题满分12分)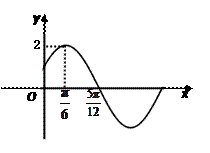
已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数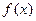 的解析式;
的解析式;
(2)令 ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.