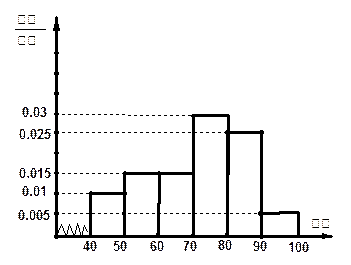（本小题满分13分）已知函数
，
，
是常数．
（1）求函数
的图象在点
处的切线方程；
（2）若函数图象上的点都在第一象限，试求常数
的取值范围；
（3）证明：
，存在
，使
．
设有关于x的一元二次方程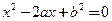
。若a是从区间[0,3]内任取的一个数，b是从区间[0,2]内任取的一个数，求上述方程没有实根的概率。
(10分)将一颗骰子（它的六个面分别标有点数1,2,3,4,5,6）先后抛掷两次，观察向上的点数，求：两数之积是6的倍数的概率；
(10分)为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测
试，将所得数据整理后，画出了频率分布直方图(如上图)，图中从左到右各小长方形面积之
比为2：4：17：15：9：3，第二小组频数为12.
（1）第二小组的频率是多少？样本容量是多少？
（2）若次数在110以上（含110次）为达标，试估计该学校全体高一学生的达标率是多少？
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球，现从甲、乙两个盒子中各取出1个球，每个球被取出的可能性相等．
（Ⅰ）求取出的两个球上标号为相同数字的概率；
（Ⅱ）求取出的两个球上标号之积能被3整除的概率．
某校从参加高一年级期末考试的学生中抽出60名学生，将其物理成绩（均为整数）分成六段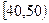
，
…
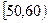后画出如下频率
分布直方图.观察图形的信息，回答下列问题：
（Ⅰ）估计这次考试的众数m与中位数n（结果保留一位小数）；
(Ⅱ)估计这次考试的及格率（60分及以上为及格）和平均分.